كيفية تطبيع مصفوفات NumPy: دليل سريع

إذا كنت تعمل مع Python لتحليل البيانات أو التعلم الآلي ، فمن المحتمل أن تصادف مصفوفات NumPy. إنها أداة قوية للتعامل مع البيانات الرقمية ، ولكن في بعض الأحيان ، تحتاج البيانات داخل هذه المصفوفات إلى تعديل أو "تطبيع" لاستخدامها بشكل فعال في الخوارزميات الخاصة بك. لكن ماذا يعني تطبيع المصفوفة؟

لتسوية مصفوفة NumPy ، يجب عليك ضبط القيم في المصفوفة بحيث تقع ضمن نطاق معين ، عادةً ما بين 0 و 1 ، أو بحيث يكون لها توزيع عادي قياسي بمتوسط ​​0 وانحراف معياري قدره 1 غالبًا ما يتم ذلك في مجال التعلم الآلي وتحليل البيانات للتأكد من أن جميع ميزات الإدخال لها نفس المقياس.

في هذه المقالة ، سوف نستكشف كيف يمكنك تطبيع مصفوفة NumPy في بايثون. سننظر في الطرق المختلفة التي يمكنك استخدامها لتطبيع مصفوفة NumPy وننظر أيضًا في أمثلة لمساعدتك على فهم المفهوم بشكل أفضل.

دعنا ندخله!

جدول المحتويات

• ما هي أساسيات التطبيع في بايثون؟
  • ما هو التطبيع؟
  • لماذا التطبيع مهم؟
  • ما هي القواعد؟
  • ما هو التطبيع في التعلم الآلي؟
• ما هي تقنيات التطبيع في بايثون؟
  • 1. كيفية إجراء تحجيم Min-Max
  • 2. كيفية إجراء تطبيع L1
  • 3. كيفية إجراء تطبيع L2
• كيفية استخدام Scikit-Learn للتطبيع في Python
  • 1. كيفية تطبيع المصفوفة باستخدام MinMaxScaler
  • 2. كيفية إجراء تسوية الصف الموضعية
• افكار اخيرة

ما هي أساسيات التطبيع في بايثون؟

قبل أن نطبق التطبيع في بايثون ، يجب أن تفهم معنى التطبيع.

لذلك ، في هذا القسم ، سوف نستعرض ما هو التطبيع ومفاهيمه الأساسية.

ما هو التطبيع؟

التطبيع هو عملية تقوم بقياس البيانات وتحويلها إلى نطاق قياسي. يتم ذلك عن طريق قسمة كل عنصر من عناصر البيانات على معلمة. يمكن أن تكون المعلمة هي الحد الأقصى للقيمة أو النطاق أو بعض المعايير الأخرى.

يمكنك تطبيع مجموعة NumPy باستخدام المعيار الإقليدي (المعروف أيضًا باسم معيار L2). علاوة على ذلك ، يمكنك أيضًا تسوية مصفوفات NumPy عن طريق إعادة قياس القيم بين نطاق معين ، عادةً من 0 إلى 1.

في Python ، توفر مكتبة NumPy طريقة فعالة لتطبيع المصفوفات. يتضمن هذا أيضًا المصفوفات والمصفوفات متعددة الأبعاد.

لماذا التطبيع مهم؟

تعد التسوية مهمة لأنها تضمن التعامل مع الميزات المختلفة على قدم المساواة عند مقارنة البيانات وتحليلها. يمكنك استخدامه للتخلص من التحيزات أو التناقضات المحتملة التي قد تنشأ بسبب المقاييس المتفاوتة.

ما هي القواعد؟

يمكن أن تكون المعلمة التي تستخدمها للتطبيع معايير مختلفة ، مثل المعيار الإقليدي (L2) أو معيار مانهاتن (L1) أو المعيار الأقصى (L_inf). أنت تستخدم المعايير لحساب حجم متجه أو مصفوفة . ثم يتم استخدام هذه كعامل قياس لتطبيع البيانات.

عند العمل مع المصفوفات ، غالبًا ما نستخدم معيار Frobenius ، وهو تعميم للمعيار الإقليدي للمصفوفات متعددة الأبعاد.

يوضح المثال التالي تطبيع المصفوفة باستخدام معيار Frobenius:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
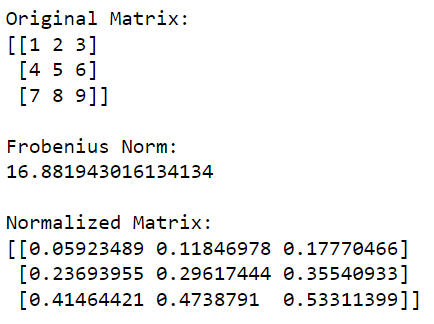
print(normalized_matrix)

سيقوم رمز Python هذا أولاً باستيراد مكتبة NumPy واستخدامها لإنشاء مصفوفة. ثم تحسب قاعدة Frobenius للمصفوفة ثم تقسم كل عنصر في المصفوفة على هذه القيمة لتطبيعها.

يتم إعطاء إخراج هذا الرمز أدناه:

ما هو التطبيع في التعلم الآلي؟

في التعلم الآلي ، يعد التطبيع خطوة مهمة للمعالجة المسبقة لأنه يحسن أداء الخوارزميات.

عند تنفيذ تقنيات التحسين القائمة على التدرج ، ستجد أن الميزات المحسّنة تميل إلى التقارب بسرعة وكفاءة أكبر. هذا لأنه يقلل من خطر التدرج السيئ أو تلاشي التدرجات.

ما هي تقنيات التطبيع في بايثون؟

يمكنك إجراء تسوية لمصفوفات NumPy بعدة طرق. ومع ذلك ، فإن بعض الطرق أكثر شيوعًا من غيرها بسبب كفاءتها العالية.

في هذا القسم ، سنلقي نظرة على تقنيات التطبيع الثلاث المستخدمة على نطاق واسع:

1. تحجيم Min-Max

2. تطبيع L1

3. تطبيع L2

1. كيفية إجراء تحجيم Min-Max

يُعرف مقياس Min-max أيضًا بالتطبيع الخطي أو تحجيم الميزة. في مقياس min-max ، نقوم بقياس قيم مصفوفة NumPy بحيث تقع ضمن نطاق محدد ، عادةً بين 0 و 1.

للقيام بذلك ، تقوم بطرح الحد الأدنى للقيمة من كل عنصر وتقسيم النتيجة على الفرق بين الحد الأقصى والحد الأدنى للقيم.

يمكنك تمثيل مقياس min-max رياضيًا على النحو التالي:

x' = (x - min(x)) / (max(x) - min(x))

يوضح المثال التالي كيف يمكنك إجراء قياس min-max باستخدام مكتبة NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

سيقوم هذا الرمز أولاً باستيراد NumPy ثم حساب الحد الأدنى والحد الأقصى للقيم في المصفوفة ، والتي يتم قياسها بعد ذلك بحيث تكون جميع القيم بين 0 (المقابلة للحد الأدنى للقيمة الأصلية) و 1 (المقابلة للقيمة القصوى الأصلية).

يتم إعطاء إخراج هذا الرمز أدناه:

مقياس Min-max هو شكل شائع جدًا من أشكال القياس في التعلم الآلي والمعالجة المسبقة للبيانات.

2. كيفية إجراء تطبيع L1

يستخدم تطبيع L1 معيار L1 ، وهو مجموع القيم المطلقة لعناصر الصفيف. هذا مفيد بشكل خاص للمصفوفات المتفرقة. يضمن أن مجموع القيم المطلقة لعناصر الصفيف المقيسة يساوي 1.

صيغة تسوية L1 هي:

x' = x / sum(|x|)

يوضح المثال التالي كيف يمكنك إجراء تسوية L1 باستخدام NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
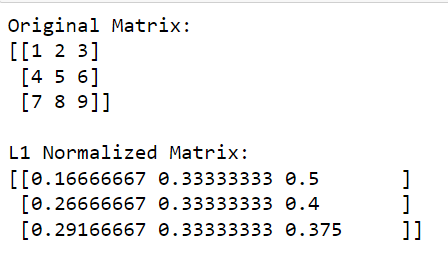
print(l1_normalized_matrix)

في هذا الكود ، يحسب np.linalg.norm (المصفوفة ، 1 ، المحور = 1 ، keepdims = True) معيار L1 لكل صف (يتم ذلك عن طريق تحديد المحور = 1).

ستعيد هذه العملية متجه عمود حيث يكون كل عنصر هو المعيار L1 للصف المقابل. بقسمة المصفوفة الأصلية على هذه المعايير (أداء عنصر القسمة) ، نحصل على نسخة L1 المقيسة من المصفوفة.

الإخراج معطى أدناه:

3. كيفية إجراء تطبيع L2

يستخدم تطبيع L2 معيار L2 ، وهو الجذر التربيعي لمجموع عناصر المصفوفة التربيعية.

تقوم هذه الطريقة بتحويل المصفوفة المقيسة إلى متجه وحدة بمعيار 2 1. يعتبر تطبيع L2 مفيدًا لتقليل الأبعاد ويضمن أهمية متساوية لجميع الميزات.

صيغة تسوية L2 هي:

x' = x / sqrt(sum(x^2))

هذه هي الطريقة التي يمكنك بها إجراء تسوية L2 باستخدام NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

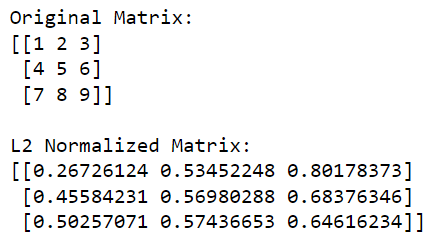
print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

في هذا الكود ، يحسب np.linalg.norm (المصفوفة ، 2 ، المحور = 1 ، keepdims = True) معيار L2 (المعيار الإقليدي) لكل صف (يتم ذلك عن طريق تحديد المحور = 1). ستعيد هذه العملية متجه عمود حيث يكون كل عنصر هو المعيار L2 للصف المقابل.

بقسمة المصفوفة الأصلية على هذه المعايير (أداء عنصر القسمة) ، نحصل على نسخة L2 المقيسة من المصفوفة.

الإخراج معطى أدناه:

حسنًا ، بعد أن تجاوزنا الطرق الشائعة لإنشاء مصفوفة طبيعية باستخدام NumPy ، دعنا نلقي نظرة على كيفية القيام بنفس الشيء باستخدام مكتبات Python الأخرى في القسم التالي.

كيفية استخدام Scikit-Learn للتطبيع في Python

Scikit-Learn هي مكتبة Python قوية للتعلم الآلي. يوفر العديد من الأدوات للمعالجة المسبقة للبيانات.

إحدى الأدوات التي يمكنك استخدامها هي وحدة sklearn.preprocessing ، والتي تقدم تقنيات متنوعة لإجراء التطبيع. هناك العديد من وظائف قشارة مختلفة ، والمحولات ، والمطابعات المتاحة. ومع ذلك ، سنركز على MinMaxScaler ووظيفة التسوية .

لمعالجة البيانات مسبقًا باستخدام scikit-learn ، فأنت تستخدم بشكل أساسي واجهة برمجة تطبيقات المحولات. يتضمن ذلك طرق الملائمة والتحويل والملاءمة .

1. كيفية تطبيع المصفوفة باستخدام MinMaxScaler

إن MinMaxScaler عبارة عن قشارة تقوم بتسوية البيانات إلى نطاق محدد ، عادة [0 ، 1].

يتم إعطاء صيغة MinMaxScalar أدناه:

scaled_value = (value - min_value) / (max_value - min_value)

لتنفيذ MinMaxScaler ، يمكنك اتباع الخطوات التالية:

1. استيراد المكتبات المطلوبة:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. قم بإنشاء مصفوفة NumPy:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. قم بإنشاء MinMaxScaler وتناسبه مع البيانات:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. قم بتحويل البيانات باستخدام أسلوب التحويل أو أسلوب التحويل المناسب :

   normalized_data = scaler.transform(data)

يتم إعطاء إخراج هذا الرمز أدناه:

كما ترى في الإخراج ، فإن MinMaxScalarMatrix له قيم تتراوح من 0 إلى 1 فقط.

2. كيفية إجراء تسوية الصف الموضعية

يمكنك أيضًا استخدام تسوية الصف الموضعية كبديل ، باستخدام وظيفة التسوية .

تعمل هذه الطريقة على تطبيع كل صفيف أو ميزة إدخال بشكل مستقل عن طريق تغيير حجم المتجه إلى معيار الوحدة. بشكل افتراضي ، تستخدم وظيفة التسوية معيار L2 لإجراء تسوية بسيطة ، ولكن يمكنك اختيار خيارات القاعدة الأخرى.

يوضح المثال التالي تسوية الصف في الموضع:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
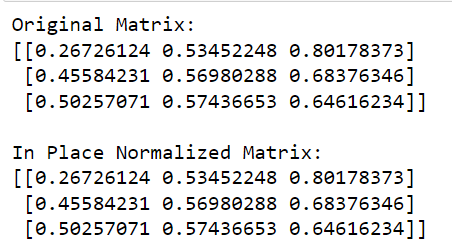
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
print(matrix)

في هذا الكود ، نسمي وظيفة التسوية من sklearn ، ونحدد القاعدة المراد استخدامها ('l2' في هذه الحالة) ، ونقوم بتعيين نسخة = خطأ لإجراء التطبيع في الموضع.

يتم إعطاء إخراج هذا الرمز أدناه:

لمعرفة المزيد حول التعلم الآلي في Python ، تحقق من الفيديو التالي:

افكار اخيرة

أثناء استكشافك لعلوم البيانات والتعلم الآلي ، ستجد أن عملية التطبيع هي خطوة أساسية في خط أنابيب المعالجة المسبقة للبيانات.

أولاً ، يضع ميزات مختلفة على مقياس مشترك. هذا يجعل نماذجك أقل حساسية لمقياس المدخلات. يمكنه تحسين أداء العديد من خوارزميات التعلم الآلي بشكل كبير.

ثانيًا ، يساعدك في تسريع عملية التدريب. تتقارب بعض الخوارزميات ، خاصة تلك التي تستند إلى حسابات المسافة المحسوبة ، بشكل أسرع عندما يتم تطبيع البيانات.

من خلال تعلم كيفية تطبيع البيانات ، فإنك تزود نفسك بمهارة حاسمة. التطبيع هو أداة عملية تستخدم بشكل روتيني في تطبيقات العالم الحقيقي. سيساعدك في تقليل احتمالية النتائج غير المتوقعة بسبب القيم المتطرفة أو الاختلافات في الوحدات.

مثل أي أداة ، يكمن مفتاح إتقان التطبيع في الممارسة. لذلك ، لا تتردد في جعل يديك متسخين وجرب مجموعات بيانات مختلفة وقيمًا عشوائية. عالم علوم البيانات هو محارتك. ترميز سعيد!