مصفوفة LuckyTemplates | كيفية إصلاح إجماليات المصفوفة في LuckyTemplates

في هذا البرنامج التعليمي ، سأوضح لك كيفية إصلاح مجاميع مصفوفة LuckyTemplates ، خاصة تحديد الإجماليات والإجماليات الفرعية إذا كانت المقاييس التي تقوم بإنشائها لا تنتج النتائج الصحيحة في الأصل. يمكنك مشاهدة الفيديو الكامل لهذا البرنامج التعليمي في أسفل هذه المدونة.

هناك سببان وراء رغبتي في معالجة هذه المشكلة. واحد هو أنه يحدث في كثير من الأحيان إلى حد ما. إنه شيء يظهر كثيرًا في . نرى هذا السؤال يتكرر مرات ومرات بأشكال مختلفة. السبب الثاني هو أنه عندما تتناولها في سياق مصفوفة ، فمن المحتمل أن تكون أصعب مشاكل الإجماليات المعطلة.

إذا تعلمت كيفية معالجتها في المصفوفة ، فستعرف ما عليك القيام به لإصلاح إجمالياتك في البطاقات والجداول وفي المرئيات الأخرى حيث قد تنكسر المجاميع. سأخوض عملية منهجية لإصلاح مجاميع مصفوفة LuckyTemplates التي تم تقسيمها بالفعل وقسمتها حسب المكونات.

في هذا المثال ، كان الإجراء معقدًا بدرجة كافية لدرجة أنه كسر المجاميع بطريقة مذهلة إلى حد ما. أردت أن أبدأ بإجماليات معطلة حقًا لأوضح لك كيفية إصلاح حتى أسوأ مشاكل الإجماليات المعطلة.

جدول المحتويات

• الإجماليات غير الصحيحة في مصفوفة LuckyTemplates
• تحديد إجماليات مصفوفة LuckyTemplates باستخدام منطق التبديل الصحيح
• التصحيح باستخدام محرر الجداول 3
• خاتمة

الإجماليات غير الصحيحة في مصفوفة LuckyTemplates

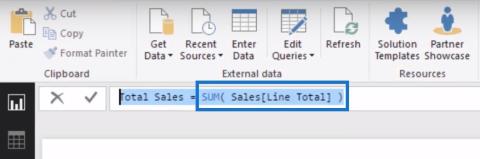
لنلقِ نظرة على سياق المقاييس في هذا المثال. أولاً ، لدينا مقياس يسمى Spread Revenue ، وهو فرع من إجمالي إيرادات الفرصة وعامل قياس البحث .

إجمالي عائد الفرصة هو مجرد مقياس بسيط ، بينما يعد عامل مقياس البحث أكثر تعقيدًا ، وهو نوع من البحث متعدد المعايير الذي نقوم به على أساس سلسلة من شروط التصفية.

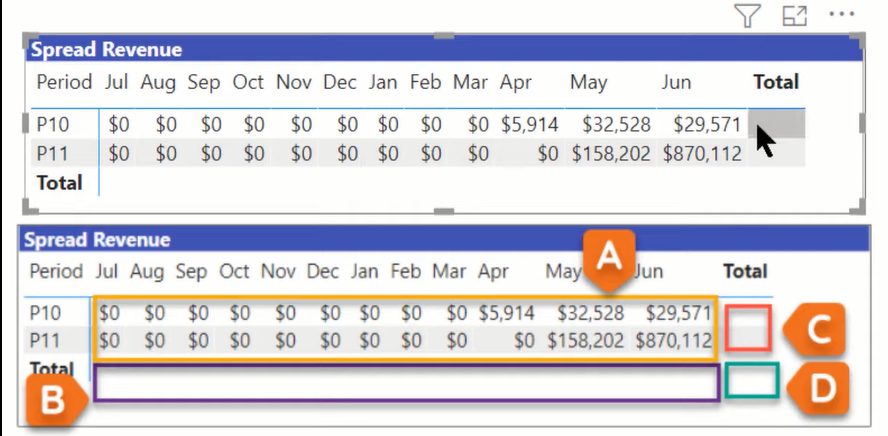
هذا مجرد مثال على طريقة يمكن أن تنكسر بها الإجماليات. الآن إذا أخذنا هذا العائد على السبريد وقمنا بإسقاطه في حقل المصفوفة ، هذا ما يحدث (انظر أدناه).

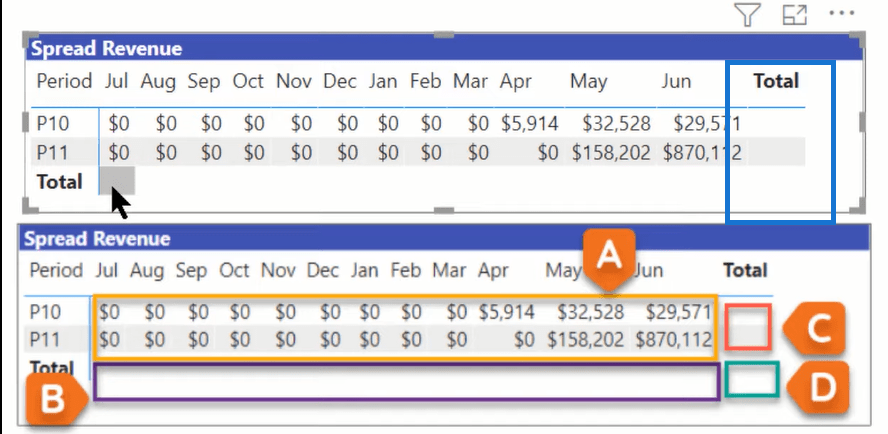
كما ترى ، يتم حساب الصفوف الأساسية بشكل صحيح ، لكن الصفوف الإجمالية لا تحسبها. في كثير من الحالات ، عندما يكون لديك إجماليات وإجماليات فرعية وإجماليات كلية ، فإن LuckyTemplates ستأخذ تخمينًا على الأقل. وفي كثير من الأحيان ، يكون هذا التخمين خاطئًا ، ويتعين عليك إصلاح المجاميع.

ولكن في هذه الحالة ، يعطي LuckyTemplates ما يعادل الاستهتار. ليس لديها أي فكرة عما يجب أن تكون عليه هذه المجاميع. ليس لديها حتى تخمين. انها مجرد تسميات تلك فارغة. لحل هذه المشكلة ، يجب أن نبني هنا بعض المنطق الإضافي الذي يخبر LuckyTemplates بما يجب فعله في مجاميع الصفوف وإجماليات الأعمدة والإجماليات الكلية.

في كثير من الحالات ، حيث تبحث في حالات متعددة ، يمكنك القيام بذلك على هيئة جملة متداخلة . لكن لدينا بنية أفضل في LuckyTemplates تجعل من السهل جدًا رؤية المنطق ، وهو عبارة .

تحديد إجماليات مصفوفة LuckyTemplates باستخدام منطق التبديل الصحيح

لدينا بيان صحيح للتبديل مبني من العام إلى الخاص ، وأريد أن أوضح لك سبب عدم نجاح ذلك. ما تفعله عبارة SWITCH TRUE هو أنها تمر عبر كل شرط من الشروط. إنه يخرج من أول واحد صحيح.

وهكذا ، في هذه الحالة ، ننتقل من الجنرال. تقول ، "إذا كانت فئة الحيوان في monotremes ، الجرابيات ، المشيمة ، عندها تحصل على تصنيف الثدييات". في هذا المثال ، هذه هي الفئات الثلاث الوحيدة للثدييات. إذا كان من الثدييات ، فسيكون أحد هذه الأنواع الثلاثة.

إذا نظرنا إلى ما يحدث ، تأتي البيانات ونذهب إلى SWITCH TRUE. وإذا كانت واحدة من هذه الفئات ، فإنها تحصل على "الثدييات". هذا يعني أنه لن ينزل أبدًا إلى هذا المعيار للجرابيات أو المعيار الذي نريده ، وهو الكنغر لأن هذه كلها ثدييات. وبالتالي ، إذا كان هذا البيان صحيحًا ، فسيتم الخروج منه.

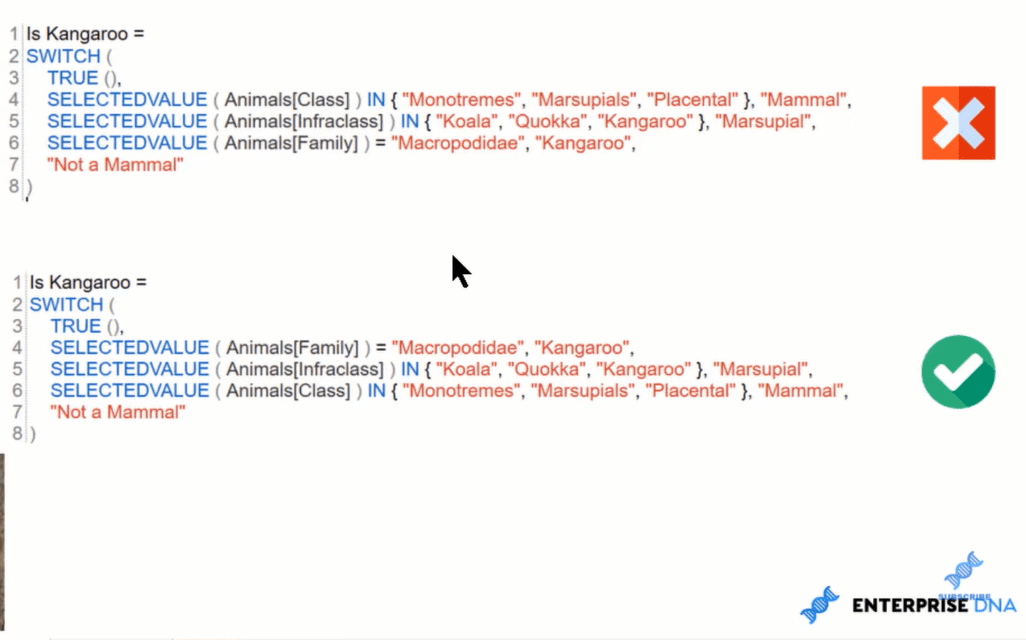
إذا كانت العبارة غير صحيحة ، فلن تكون العبارتان صحيحتين. سيذهب إلى الوضع الافتراضي ، وهو ليس من الثدييات. لذا فبدلاً من البناء من العام إلى الخاص ، عليك إنشاء بيان SWITCH TRUE من الخاص إلى العام ، ثم تجميع الكل في النهاية.

إذا رجعنا بهذا إلى مثال إصلاح مجاميع المصفوفات ، فهو في الحقيقة نفس الشيء. A هنا هي التفاصيل ، والتي ستكون أول بيان في SWITCH TRUE. وبعد ذلك ، لدينا D باعتباره عاملاً شاملاً. في المنتصف ، لدينا شرطان B و C. يحتوي B على سياق العمود ، ولكن ليس الصف ، بينما يحتوي C على سياق للصف ، ولكن ليس العمود.

الآن دعنا ننتقل إلى Tabular Editor 3 (TE3) ، وهي حقًا طريقتي المفضلة الآن لتصحيح الأخطاء وفهم الإجراءات.

التصحيح باستخدام محرر الجداول 3

أسمي هذا المقياس (أدناه) إيراد السبريد مع الإجماليات الثابتة. إنها طويلة جدًا وتبدو مثل DAX المعقد ، لكنني سأقوم بتقسيم هذا حسب المكون.

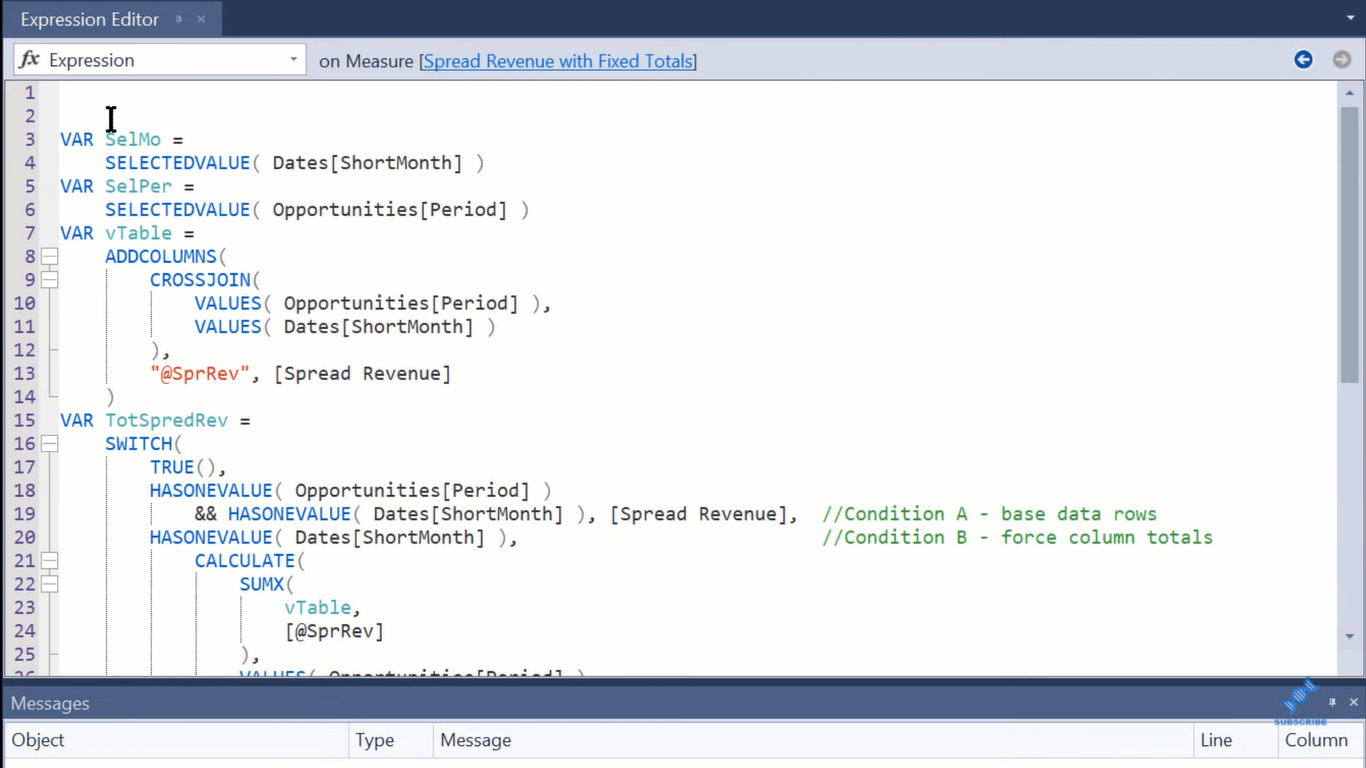
لدينا هنا متغيرين فقط يلتقطان أساسًا SELECTEDVALUE القصير وفترة عملنا ، وهذا سيحدد السياق. بعد ذلك ، لدينا جدول افتراضي ، وهو في الأساس نسخة افتراضية من المصفوفة من خلال بناء و .

إذا نظرنا إلى هذا داخل استعلام DAX ، يمكنك أن ترى أنه يقوم بشكل أساسي بإنشاء كل مجموعة ممكنة من الفترة والشهر القصير ، وهو ما تفعله المصفوفة.

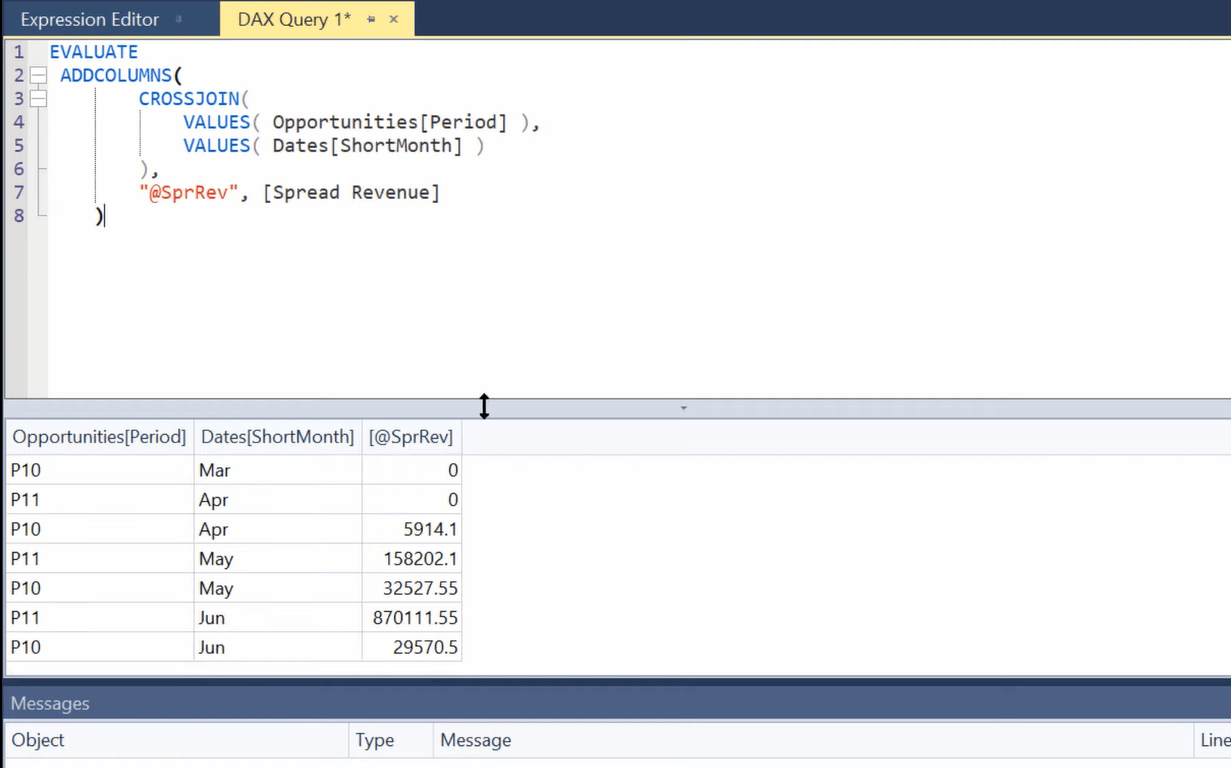
داخل Tabular Editor 3 ، هناك طريقة أخرى لتصور هذا تسمى Pivot Grid. إنها تنتج صورة بصرية تساوي تلك المصفوفة المرئية في LuckyTemplates.

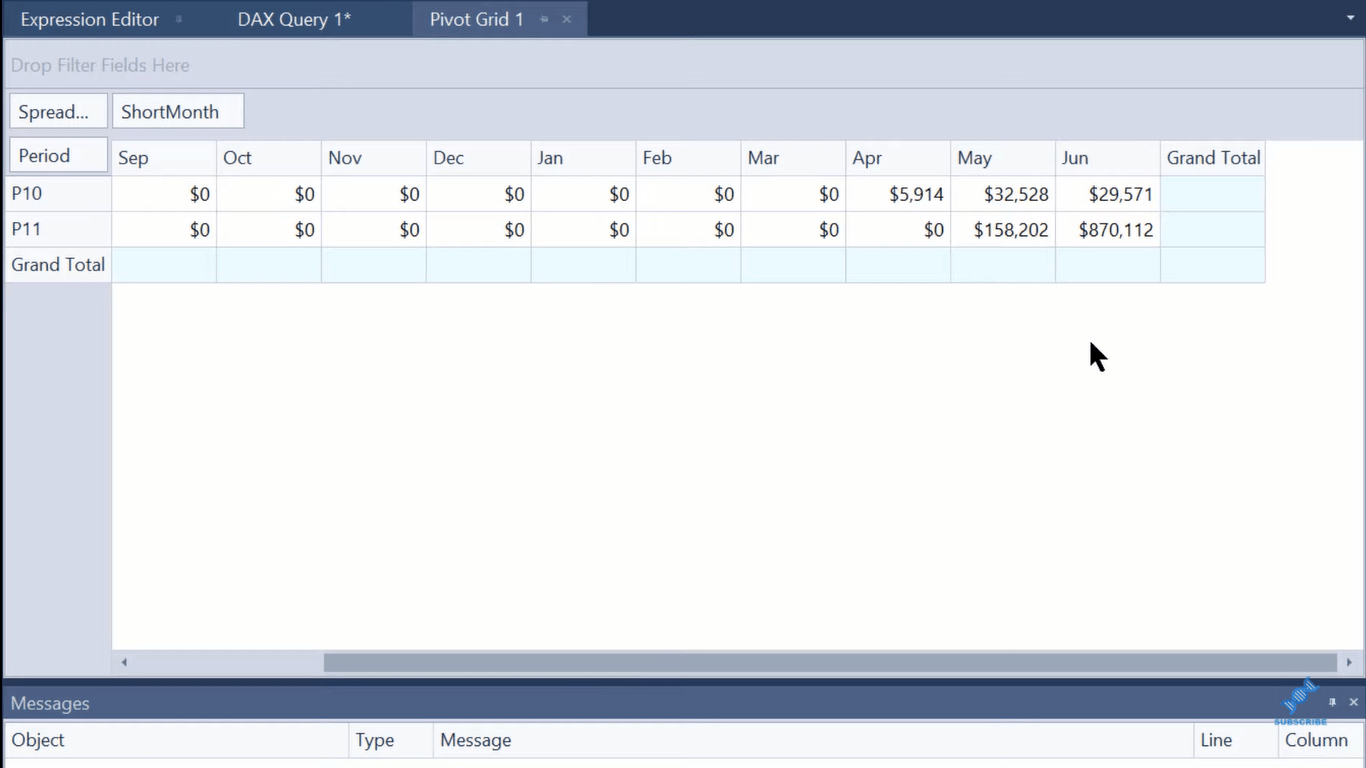
بالعودة إلى القياس الخاص بنا في محرر التعبير ، نحتاج إلى بناء المنطق الذي ينشئ حقول الإجماليات. وهكذا ، لدينا بيان SWITCH TRUE هذا مع ، حيث نقوم باختبار لمعرفة ما إذا كان هناك سياق في كل من الحقلين نحتاج إلى سياق فيه.

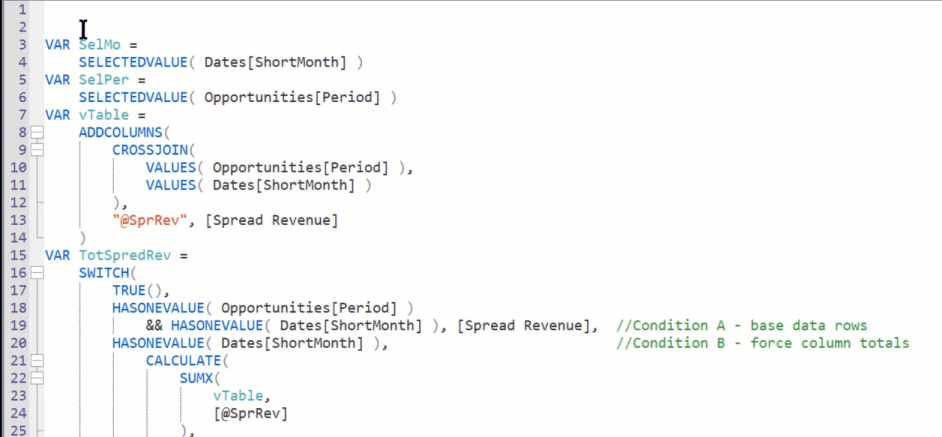
الشرط الأول ، الذي يكون من الأكثر تحديدًا إلى الأقل تحديدًا ، هو الشرط أ ، الصفوف الأساسية. لذلك ، إذا كان لدينا سياق لفترة ولدينا سياق للشهر القصير ، فإننا نستخدم مقياس فروق الإيرادات فقط لأن ذلك كان ينتج النتائج الصحيحة في صفوف البيانات هذه.

نحتاج الآن إلى بناء منطق B ، حيث لدينا سياق في العمود. لذلك ، لدينا HASONEVALUE للشهر القصير ، ولكن ليس لفترة. الآن نريد أن نفرض المنطق ، ونأخذ المصفوفة الافتراضية ، ونأخذ مقياس السبريد الخاص بنا ، ثم نجمعه عبر جميع قيم الفترة.

الشيء التالي الذي لدينا هو الجانب الآخر ، حيث لدينا HASONEVALUE في فترة ، ولكن ليس في شهر قصير. نأخذ الآن للجدول الافتراضي (مقياس إيراد السبريد) ، ونلخصه في جميع الشهر القصير.

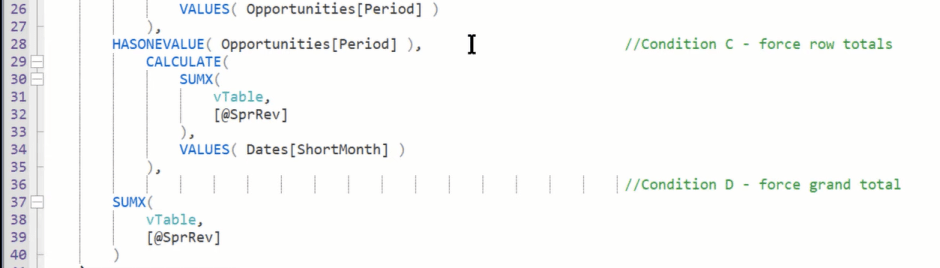
ثم أخيرًا ، لدينا مقياس شامل ، وهو أنه إذا لم يكن لدينا سياق في أي من الاثنين ، فإننا نأخذ المجموع الكلي للجدول الافتراضي.

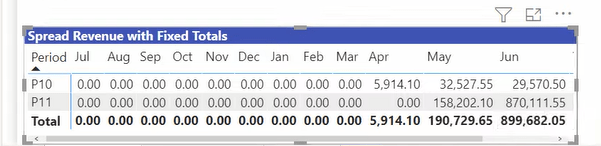
الآن إذا أخذنا قياس إيراد الفروق مع الإجماليات الثابتة إلى الحقول وقمنا بإسقاطه في القيم ، فإننا نحصل على الإجماليات المناسبة لإجماليات الصفوف وإجماليات الأعمدة والإجماليات الكلية. يمر منطق SWITCH TRUE ويفرض كل المنطق الذي نحتاجه للحصول على الإجماليات الصحيحة.

كيفية إنشاء مجاميع فرعية فريدة في جداول LuckyTemplates
إصلاح الإجماليات غير الصحيحة باستخدام مقاييس DAX في LuckyTemplates
باستخدام المنطق المتقدم في LuckyTemplates لتصحيح الإجماليات

خاتمة

في هذه المدونة ، أوضحت لك كيفية إصلاح الإجماليات غير الصحيحة في مصفوفة LuckyTemplates. هذا هو البناء الذي يمكنك فرضه على طاولة أو على بطاقة ، حيث تقوم ببناء المنطق الافتراضي للصفوف الأساسية ، والذي سيعمل عادةً إذا كان لديك مقياس صحيح. وبعد ذلك ، ما عليك سوى فرض المنطق الذي تحتاجه لفرض المجموع الصحيح.

يبدو معقدًا ولكنه مفيد بالتأكيد. آمل أن يكون كل هذا واضحًا. يمكنك مشاهدة الفيديو التعليمي الكامل أدناه والتحقق من الروابط لمزيد من المحتوى ذي الصلة.

أتمنى لك كل خير!