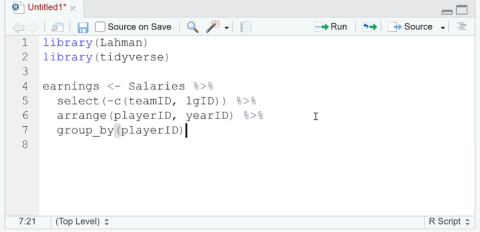
Dodawaj, usuwaj i zmieniaj nazwy kolumn w R za pomocą Dplyr
W tym samouczku omówimy pakiet dplyr, który umożliwia sortowanie, filtrowanie, dodawanie i zmianę nazw kolumn w języku R.
Jeśli pracowałeś z Pythonem do analizy danych lub uczenia maszynowego, prawdopodobnie natknąłeś się na tablice NumPy. Są potężnym narzędziem do obsługi danych liczbowych, ale czasami dane w tych tablicach wymagają dostosowania lub „znormalizowania”, aby można je było skutecznie wykorzystać w algorytmach. Ale co to znaczy normalizować tablicę?
Aby znormalizować tablicę NumPy, musisz dopasować wartości w tablicy tak, aby mieściły się w określonym zakresie, zazwyczaj między 0 a 1, lub aby miały standardowy rozkład normalny ze średnią 0 i odchyleniem standardowym 1 Odbywa się to często w dziedzinie uczenia maszynowego i analizy danych, aby zapewnić, że wszystkie cechy wejściowe mają tę samą skalę.

W tym artykule przyjrzymy się, jak można znormalizować tablicę NumPy w Pythonie. Przyjrzymy się różnym metodom normalizacji tablicy NumPy, a także przyjrzymy się przykładom, które pomogą lepiej zrozumieć tę koncepcję.
Wejdźmy w to!
Spis treści
Jakie są podstawy normalizacji w Pythonie?
Zanim zaimplementujemy normalizację w Pythonie, musisz zrozumieć, co oznacza normalizacja.

Dlatego w tej sekcji omówimy, czym jest normalizacja i jakie są jej podstawowe koncepcje.
Co to jest normalizacja?
Normalizacja to proces, który skaluje i przekształca dane w znormalizowany zakres. Odbywa się to poprzez podzielenie każdego elementu danych przez parametr. Parametrem może być wartość maksymalna, zakres lub inna norma.
Możesz znormalizować tablicę NumPy za pomocą normy euklidesowej (znanej również jako norma L2). Co więcej, możesz także znormalizować tablice NumPy, przeskalowując wartości z określonego zakresu, zwykle od 0 do 1.
W Pythonie biblioteka NumPy zapewnia efektywny sposób normalizacji tablic. Obejmuje to również wielowymiarowe tablice i macierze.
Dlaczego normalizacja jest ważna?
Normalizacja jest ważna, ponieważ zapewnia równe traktowanie różnych funkcji podczas porównywania i analizowania danych. Możesz go użyć do wyeliminowania potencjalnych odchyleń lub rozbieżności, które mogą powstać z powodu różnych skal.
Czym są normy?
Parametrem używanym do normalizacji mogą być różne normy , takie jak norma euklidesowa (L2), norma Manhattanu (L1) lub norma maksymalna (L_inf). Normy służą do obliczania wielkości wektora lub macierzy . Są one następnie wykorzystywane jako współczynnik skalowania do normalizacji danych.
Podczas pracy z macierzami często używamy normy Frobeniusa , która jest uogólnieniem normy euklidesowej dla tablic wielowymiarowych.
Poniższy przykład pokazuje normalizację macierzy przy użyciu normy Frobeniusa:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')
# Normalize the matrix
normalized_matrix = matrix / frobenius_norm
print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
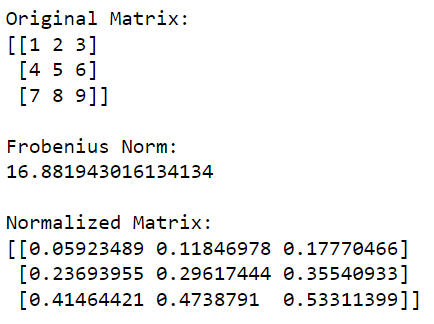
print(normalized_matrix)Ten kod Pythona najpierw zaimportuje bibliotekę NumPy i użyje jej do utworzenia macierzy. Następnie oblicza normę Frobeniusa macierzy, a następnie dzieli każdy element macierzy przez tę wartość, aby ją znormalizować.
Dane wyjściowe tego kodu podano poniżej:
Czym jest normalizacja w uczeniu maszynowym?
W uczeniu maszynowym normalizacja jest ważnym etapem przetwarzania wstępnego, ponieważ poprawia wydajność algorytmów.
Podczas wykonywania technik optymalizacji opartych na gradiencie przekonasz się, że zoptymalizowane funkcje mają tendencję do szybszego i wydajniejszego zbiegania się. Dzieje się tak, ponieważ zmniejsza ryzyko złego skalowania lub znikających gradientów.
Jakie są techniki normalizacji w Pythonie?
Normalizację tablic NumPy można przeprowadzić na wiele sposobów. Jednak niektóre metody są bardziej popularne niż inne ze względu na ich wysoką skuteczność.
W tej sekcji przyjrzymy się trzem szeroko stosowanym technikom normalizacji:
Skalowanie min-maks
Normalizacja L1
Normalizacja L2
1. Jak wykonać skalowanie min-maks
Skalowanie min-max jest również znane jako normalizacja liniowa lub skalowanie funkcji. W skalowaniu min-max skalujemy wartości tablicy NumPy tak, aby mieściły się w określonym zakresie, zwykle między 0 a 1.
W tym celu od każdego elementu odejmuje się wartość minimalną i dzieli wynik przez różnicę między wartościami maksymalnymi i minimalnymi.
Skalowanie min-max można przedstawić matematycznie jako:
x' = (x - min(x)) / (max(x) - min(x))Poniższy przykład ilustruje sposób skalowania min-max przy użyciu biblioteki NumPy:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)
scaled_matrix = (matrix - min_val) / (max_val - min_val)
print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)Ten kod najpierw zaimportuje NumPy, a następnie obliczy minimalne i maksymalne wartości w macierzy, które następnie przeskaluje w taki sposób, aby wszystkie wartości mieściły się w przedziale od 0 (odpowiadające oryginalnej wartości minimalnej) do 1 (odpowiadające oryginalnej wartości maksymalnej).
Dane wyjściowe tego kodu podano poniżej:

Skalowanie min-max jest bardzo powszechną formą skalowania w uczeniu maszynowym i wstępnym przetwarzaniu danych.
2. Jak przeprowadzić normalizację L1
Normalizacja L1 wykorzystuje normę L1, która jest sumą wartości bezwzględnych elementów tablicy. Jest to szczególnie przydatne w przypadku rzadkich macierzy. Zapewnia, że suma wartości bezwzględnych znormalizowanych elementów tablicy jest równa 1.
Wzór na normalizację L1 to:
x' = x / sum(|x|)Poniższy przykład pokazuje, jak można przeprowadzić normalizację L1 za pomocą NumPy:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm
print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
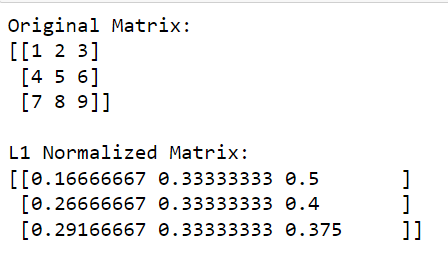
print(l1_normalized_matrix)W tym kodzie np.linalg.norm (matrix, 1, axis=1, keepdims=True) oblicza normę L1 dla każdego wiersza (odbywa się to poprzez podanie osi=1).
Ta operacja zwróci wektor kolumnowy, w którym każdy element jest normą L1 odpowiedniego wiersza. Dzieląc oryginalną macierz przez te normy (dokonując podziału elementarnego), otrzymujemy znormalizowaną wersję macierzy L1.
Dane wyjściowe podano poniżej:
3. Jak przeprowadzić normalizację L2
Normalizacja L2 wykorzystuje normę L2, która jest pierwiastkiem kwadratowym z sumy kwadratów elementów tablicy.
Ta metoda przekształca znormalizowaną tablicę w wektor jednostkowy z normą 2 równą 1. Normalizacja L2 jest przydatna do redukcji wymiarów i zapewnia równe znaczenie dla wszystkich cech.
Wzór na normalizację L2 to:
x' = x / sqrt(sum(x^2))W ten sposób możesz przeprowadzić normalizację L2 za pomocą NumPy :
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm
print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
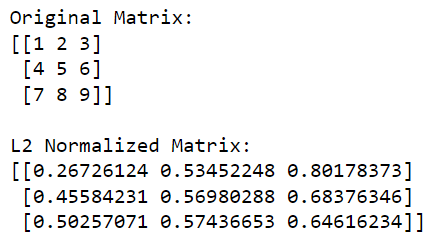
print(l2_normalized_matrix)W tym kodzie np.linalg.norm(matrix, 2, axis=1, keepdims=True) oblicza normę L2 (norma euklidesowa) dla każdego wiersza (odbywa się to poprzez określenie osi=1). Ta operacja zwróci wektor kolumnowy, w którym każdy element jest normą L2 odpowiedniego wiersza.
Dzieląc oryginalną macierz przez te normy (dokonując podziału elementarnego), otrzymujemy znormalizowaną wersję macierzy L2.
Dane wyjściowe podano poniżej:
W porządku, teraz, gdy omówiliśmy popularne sposoby tworzenia znormalizowanej tablicy przy użyciu NumPy, przyjrzyjmy się, jak możesz zrobić to samo przy użyciu innych bibliotek Pythona w następnej sekcji.
Jak używać Scikit-Learn do normalizacji w Pythonie
Scikit-learn to potężna biblioteka Pythona do uczenia maszynowego. Zapewnia kilka narzędzi do wstępnego przetwarzania danych.
Jednym z narzędzi, których możesz użyć, jest moduł sklearn.preprocessing , który oferuje różne techniki przeprowadzania normalizacji. Dostępnych jest wiele różnych funkcji skalujących, transformatorów i normalizatorów. Skupimy się jednak na MinMaxScaler i funkcji normalize .
Aby wstępnie przetworzyć dane za pomocą scikit-learn, używasz głównie interfejsu API transformatora. Obejmuje to metody fit , transform i fit_transform .
1. Jak znormalizować tablicę za pomocą MinMaxScaler
MinMaxScaler to skaler, który normalizuje dane do określonego zakresu, zwykle [0, 1] .
Wzór na MinMaxScalar podano poniżej:
scaled_value = (value - min_value) / (max_value - min_value)Aby zaimplementować MinMaxScaler , możesz wykonać następujące kroki:
Zaimportuj wymagane biblioteki:
import numpy as np
from sklearn.preprocessing import MinMaxScalerUtwórz tablicę NumPy:
data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])Utwórz instancję MinMaxScaler i dopasuj ją do danych:
scaler = MinMaxScaler()
scaler.fit(data)Przekształć dane za pomocą metody transform lub fit_transform :
normalized_data = scaler.transform(data)Dane wyjściowe tego kodu podano poniżej:

Jak widać na wyjściu, MinMaxScalarMatrix ma tylko wartości z zakresu od 0 do 1.
2. Jak przeprowadzić normalizację wierszy w miejscu
Alternatywnie można również użyć normalizacji wierszy w miejscu, używając funkcji normalizacji .
Ta metoda normalizuje każdą tablicę wejściową lub funkcję niezależnie, skalując wektor do normy jednostkowej. Domyślnie funkcja normalizacji używa normy L2 do przeprowadzenia prostej normalizacji, ale można wybrać inne opcje norm.
Poniższy przykład ilustruje normalizację wierszy w miejscu:
from sklearn.preprocessing import normalize
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)
print('L2 Normalized Matrix:')
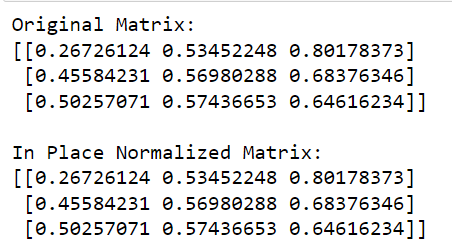
print(matrix)W tym kodzie wywołujemy funkcję normalize z sklearn , definiujemy normę do użycia (w tym przypadku „l2”) i ustawiamy copy=False , aby przeprowadzić normalizację w miejscu.
Dane wyjściowe tego kodu podano poniżej:
Aby dowiedzieć się więcej o uczeniu maszynowym w Pythonie , obejrzyj poniższy film:
Końcowe przemyślenia
W miarę dalszego poznawania nauki o danych i uczenia maszynowego przekonasz się, że proces normalizacji jest niezbędnym krokiem w potoku wstępnego przetwarzania danych.
Po pierwsze, umieszcza różne cechy na wspólnej skali. To sprawia, że modele są mniej wrażliwe na skalę danych wejściowych. Może znacznie poprawić wydajność wielu algorytmów uczenia maszynowego.
Po drugie, pomaga przyspieszyć proces szkolenia. Niektóre algorytmy, zwłaszcza te oparte na obliczeniach odległości, osiągają zbieżność szybciej, gdy dane są znormalizowane.
Ucząc się, jak normalizować dane, wyposażasz się w kluczową umiejętność. Normalizacja jest praktycznym narzędziem używanym rutynowo w rzeczywistych aplikacjach. Pomoże Ci to zmniejszyć prawdopodobieństwo nieoczekiwanych wyników z powodu wartości odstających lub różnic w jednostkach.
Jak każde narzędzie, klucz do opanowania normalizacji leży w praktyce. Więc nie wahaj się ubrudzić sobie rąk i eksperymentować z różnymi zestawami danych i losowymi wartościami. Świat nauki o danych jest Twoją ostrygą. Miłego kodowania!
W tym samouczku omówimy pakiet dplyr, który umożliwia sortowanie, filtrowanie, dodawanie i zmianę nazw kolumn w języku R.
Odkryj różnorodne funkcje zbierania, które można wykorzystać w Power Automate. Zdobądź praktyczne informacje o funkcjach tablicowych i ich zastosowaniu.
Z tego samouczka dowiesz się, jak ocenić wydajność kodów DAX przy użyciu opcji Uruchom test porównawczy w DAX Studio.
Czym jest self w Pythonie: przykłady z życia wzięte
Dowiesz się, jak zapisywać i ładować obiekty z pliku .rds w R. Ten blog będzie również omawiał sposób importowania obiektów z R do LuckyTemplates.
Z tego samouczka języka kodowania DAX dowiesz się, jak używać funkcji GENERUJ i jak dynamicznie zmieniać tytuł miary.
W tym samouczku omówiono sposób korzystania z techniki wielowątkowych wizualizacji dynamicznych w celu tworzenia szczegółowych informacji na podstawie dynamicznych wizualizacji danych w raportach.
W tym artykule omówię kontekst filtra. Kontekst filtrowania to jeden z głównych tematów, z którym każdy użytkownik usługi LuckyTemplates powinien zapoznać się na początku.
Chcę pokazać, jak usługa online LuckyTemplates Apps może pomóc w zarządzaniu różnymi raportami i spostrzeżeniami generowanymi z różnych źródeł.
Dowiedz się, jak obliczyć zmiany marży zysku przy użyciu technik, takich jak rozgałęzianie miar i łączenie formuł języka DAX w usłudze LuckyTemplates.