Cara Menormalkan Tatasusunan NumPy: Panduan Pantas

Jika anda telah bekerja dengan Python untuk analisis data atau pembelajaran mesin, anda mungkin menjumpai tatasusunan NumPy. Ia adalah alat yang berkuasa untuk mengendalikan data berangka, tetapi kadangkala, data dalam tatasusunan ini perlu dilaraskan atau 'dinormalkan' untuk digunakan dengan berkesan dalam algoritma anda. Tetapi apakah yang dimaksudkan untuk menormalkan tatasusunan?

Untuk menormalkan tatasusunan NumPy, anda perlu melaraskan nilai dalam tatasusunan supaya ia berada dalam julat tertentu, biasanya antara 0 dan 1, atau supaya ia mempunyai taburan normal piawai dengan min 0 dan sisihan piawai 1 Ini sering dilakukan dalam bidang pembelajaran mesin dan analisis data untuk memastikan semua ciri input mempunyai skala yang sama.

Dalam artikel ini, kami akan meneroka cara anda boleh menormalkan tatasusunan NumPy dalam Python. Kami akan melihat kaedah berbeza yang boleh anda gunakan untuk menormalkan tatasusunan NumPy dan juga melihat contoh untuk membantu anda memahami konsep dengan lebih baik.

Mari kita masuk ke dalamnya!

Isi kandungan

• Apakah Asas Normalisasi dalam Python?
  • Apakah Normalisasi?
  • Mengapa Normalisasi Penting?
  • Apakah Norma?
  • Apakah Normalisasi dalam Pembelajaran Mesin?
• Apakah Teknik Normalisasi dalam Python?
  • 1. Cara Melakukan Penskalaan Min-Max
  • 2. Cara Melakukan Normalisasi L1
  • 3. Cara Melakukan Normalisasi L2
• Cara Menggunakan Scikit-Learn untuk Normalisasi dalam Python
  • 1. Cara Menormalkan Tatasusunan Menggunakan MinMaxScaler
  • 2. Cara Melakukan Normalisasi Baris Di Tempat
• Fikiran Akhir

Apakah Asas Normalisasi dalam Python?

Sebelum kita melaksanakan normalisasi dalam Python, anda mesti memahami maksud normalisasi.

Oleh itu, dalam bahagian ini, kita akan membincangkan apa itu normalisasi dan konsep terasnya.

Apakah Normalisasi?

Normalisasi ialah proses yang menskalakan dan mengubah data menjadi julat piawai. Ini dilakukan dengan membahagikan setiap elemen data dengan parameter. Parameter boleh menjadi nilai maksimum, julat atau beberapa norma lain.

Anda boleh menormalkan tatasusunan NumPy menggunakan norma Euclidean (juga dikenali sebagai norma L2). Tambahan pula, anda juga boleh menormalkan tatasusunan NumPy dengan menskala semula nilai antara julat tertentu, biasanya 0 hingga 1.

Dalam Python, perpustakaan NumPy menyediakan cara yang cekap untuk menormalkan tatasusunan. Ini termasuk tatasusunan berbilang dimensi dan matriks juga.

Mengapa Normalisasi Penting?

Normalisasi adalah penting kerana ia memastikan ciri yang berbeza dilayan sama rata apabila membandingkan dan menganalisis data. Anda boleh menggunakannya untuk menghapuskan potensi berat sebelah atau percanggahan yang mungkin timbul disebabkan oleh skala yang berbeza-beza.

Apakah Norma?

Parameter yang anda gunakan untuk normalisasi boleh menjadi norma yang berbeza , seperti norma Euclidean (L2), norma Manhattan (L1), atau norma maks (L_inf). Anda menggunakan norma untuk mengira magnitud vektor atau matriks . Ini kemudiannya digunakan sebagai faktor penskalaan untuk menormalkan data.

Apabila bekerja dengan matriks, kita sering menggunakan norma Frobenius , yang merupakan generalisasi norma Euclidean untuk tatasusunan berbilang dimensi.

Contoh berikut menunjukkan penormalan matriks menggunakan norma Frobenius:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
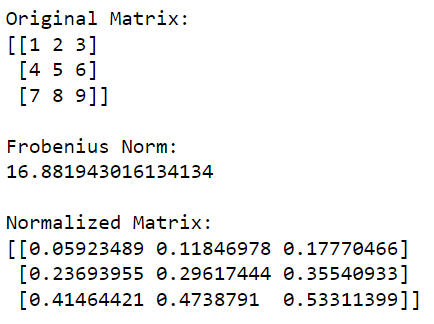
print(normalized_matrix)

Kod Python ini akan mengimport perpustakaan NumPy dahulu dan menggunakannya untuk mencipta matriks. Ia kemudian mengira norma Frobenius matriks dan kemudian membahagikan setiap elemen dalam matriks dengan nilai ini untuk menormalkannya.

Output kod ini diberikan di bawah:

Apakah Normalisasi dalam Pembelajaran Mesin?

Dalam pembelajaran mesin , normalisasi ialah langkah prapemprosesan yang penting kerana ia meningkatkan prestasi algoritma.

Apabila melakukan teknik pengoptimuman berasaskan kecerunan, anda akan mendapati ciri yang dioptimumkan cenderung untuk menumpu dengan lebih cepat dan cekap. Ini kerana ia mengurangkan risiko penskalaan yang lemah atau kecerunan yang hilang.

Apakah Teknik Normalisasi dalam Python?

Anda boleh melakukan normalisasi tatasusunan NumPy dalam beberapa cara. Walau bagaimanapun, beberapa kaedah lebih popular daripada yang lain kerana kecekapannya yang tinggi.

Untuk bahagian ini, kita akan melihat tiga teknik normalisasi yang digunakan secara meluas:

1. Penskalaan Min-Max

2. L1 Normalisasi

3. L2 Normalisasi

1. Cara Melakukan Penskalaan Min-Max

Penskalaan min-maks juga dikenali sebagai penormalan linear atau penskalaan ciri. Dalam penskalaan min-maks, kami menskalakan nilai tatasusunan NumPy supaya nilai tersebut berada dalam julat yang ditentukan, biasanya antara 0 dan 1.

Untuk melakukan ini, anda menolak nilai minimum daripada setiap elemen dan membahagikan hasilnya dengan perbezaan antara nilai maksimum dan minimum.

Anda boleh mewakili penskalaan min-maks secara matematik sebagai:

x' = (x - min(x)) / (max(x) - min(x))

Contoh berikut menunjukkan cara anda boleh melakukan penskalaan min-maks menggunakan perpustakaan NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Kod ini mula-mula akan mengimport NumPy dan kemudian mengira nilai minimum dan maksimum dalam matriks, yang kemudiannya diskalakan supaya semua nilai adalah antara 0 (bersamaan dengan nilai minimum asal) dan 1 (bersamaan dengan nilai maksimum asal).

Output kod ini diberikan di bawah:

Penskalaan min-maks ialah bentuk penskalaan yang sangat biasa dalam pembelajaran mesin dan prapemprosesan data.

2. Cara Melakukan Normalisasi L1

Normalisasi L1 menggunakan norma L1, iaitu jumlah nilai mutlak elemen tatasusunan. Ini amat berguna untuk matriks jarang. Ia memastikan bahawa jumlah nilai mutlak unsur tatasusunan ternormal adalah sama dengan 1.

Formula untuk normalisasi L1 ialah:

x' = x / sum(|x|)

Contoh berikut menunjukkan cara anda boleh melakukan penormalan L1 menggunakan NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
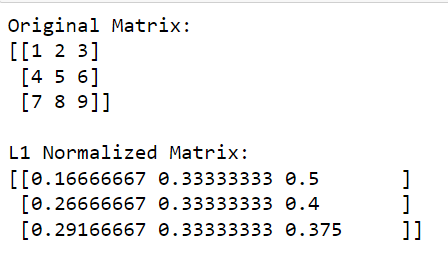
print('nL1 Normalized Matrix:')
print(l1_normalized_matrix)

Dalam kod ini, np.linalg.norm (matriks, 1, axis=1, keepdims=True) mengira norma L1 untuk setiap baris (ini dilakukan dengan menyatakan paksi=1).

Operasi ini akan mengembalikan vektor lajur di mana setiap elemen ialah norma L1 bagi baris yang sepadan. Dengan membahagikan matriks asal dengan norma-norma ini (melakukan pembahagian mengikut unsur), kami memperoleh versi matriks ternormal L1.

Output diberikan di bawah:

3. Cara Melakukan Normalisasi L2

Normalisasi L2 menggunakan norma L2, iaitu punca kuasa dua jumlah unsur tatasusunan kuasa dua.

Kaedah ini menukar tatasusunan ternormal kepada vektor unit dengan 2-norma 1. Normalisasi L2 berguna untuk pengurangan dimensi dan memastikan kepentingan yang sama untuk semua ciri.

Formula untuk normalisasi L2 ialah:

x' = x / sqrt(sum(x^2))

Inilah cara anda boleh melakukan normalisasi L2 menggunakan NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
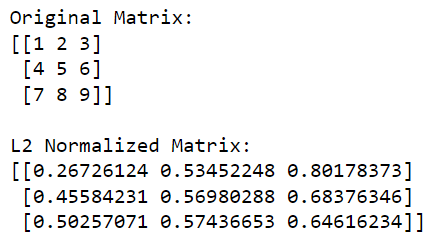
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

Dalam kod ini, np.linalg.norm(matriks, 2, axis=1, keepdims=True) mengira norma L2 (norma Euclidean) untuk setiap baris (ini dilakukan dengan menyatakan paksi=1). Operasi ini akan mengembalikan vektor lajur di mana setiap elemen ialah norma L2 bagi baris yang sepadan.

Dengan membahagikan matriks asal dengan norma-norma ini (melakukan pembahagian mengikut unsur), kami memperoleh versi matriks ternormal L2.

Output diberikan di bawah:

Baiklah, sekarang kita telah membincangkan cara popular untuk mencipta tatasusunan ternormal menggunakan NumPy, mari kita lihat cara anda boleh melakukan perkara yang sama menggunakan perpustakaan Python lain dalam bahagian seterusnya.

Cara Menggunakan Scikit-Learn untuk Normalisasi dalam Python

Scikit-learn ialah perpustakaan Python yang berkuasa untuk pembelajaran mesin. Ia menyediakan beberapa alat untuk prapemprosesan data.

Satu alat yang boleh anda gunakan ialah modul sklearn.preprocessing , yang menawarkan pelbagai teknik untuk melakukan normalisasi. Terdapat banyak fungsi penimbang, transformer dan penormal yang berbeza tersedia. Walau bagaimanapun, kami akan menumpukan pada MinMaxScaler dan fungsi normalize .

Untuk pramemproses data dengan scikit-learn, anda menggunakan API transformer terutamanya. Ini termasuk kaedah fit , transform , dan fit_transform .

1. Cara Menormalkan Tatasusunan Menggunakan MinMaxScaler

MinMaxScaler ialah penimbang yang menormalkan data kepada julat tertentu, biasanya [0, 1] .

Formula untuk MinMaxScalar diberikan di bawah:

scaled_value = (value - min_value) / (max_value - min_value)

Untuk melaksanakan MinMaxScaler , anda boleh mengikuti langkah berikut:

1. Import perpustakaan yang diperlukan:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Buat tatasusunan NumPy:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Segerakan MinMaxScaler dan muatkannya dengan data:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Ubah data menggunakan kaedah transform atau fit_transform :

   normalized_data = scaler.transform(data)

Output kod ini diberikan di bawah:

Seperti yang anda lihat dalam output bahawa MinMaxScalarMatrix hanya mempunyai nilai antara 0 hingga 1.

2. Cara Melakukan Normalisasi Baris Di Tempat

Anda juga boleh menggunakan normalisasi baris di tempat sebagai alternatif, menggunakan fungsi normalize .

Kaedah ini menormalkan setiap tatasusunan input atau ciri secara bebas dengan menskalakan vektor kepada norma unit. Secara lalai, fungsi normalize menggunakan norma L2 untuk melakukan normalisasi mudah, tetapi anda boleh memilih pilihan norma lain.

Contoh berikut menunjukkan normalisasi baris di tempat:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

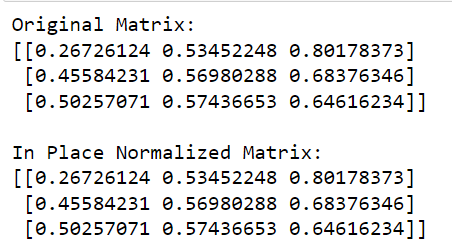
print('L2 Normalized Matrix:')
print(matrix)

Dalam kod ini, kami memanggil fungsi normalize daripada sklearn , tentukan norma untuk digunakan ('l2' dalam kes ini), dan tetapkan copy=False untuk melakukan normalisasi di tempat.

Output kod ini diberikan di bawah:

Untuk mengetahui lebih lanjut tentang pembelajaran mesin dalam Python , lihat video berikut:

Fikiran Akhir

Sambil anda meneroka lebih lanjut sains data dan pembelajaran mesin, anda akan mendapati bahawa proses penormalan ialah langkah penting dalam saluran paip prapemprosesan data anda.

Pertama, ia meletakkan ciri yang berbeza pada skala yang sama. Ini menjadikan model anda kurang sensitif terhadap skala input. Ia boleh meningkatkan prestasi banyak algoritma pembelajaran mesin.

Kedua, ia membantu anda dalam mempercepatkan proses latihan. Sesetengah algoritma, terutamanya yang berdasarkan pengiraan jarak yang dikira, menumpu lebih cepat apabila data dinormalkan.

Dengan mempelajari cara menormalkan data, anda melengkapkan diri anda dengan kemahiran penting. Normalisasi ialah alat praktikal yang digunakan secara rutin dalam aplikasi dunia sebenar. Ia akan membantu anda dalam mengurangkan kemungkinan hasil yang tidak dijangka disebabkan oleh outlier atau perbezaan dalam unit.

Seperti mana-mana alat, kunci untuk menguasai normalisasi terletak pada amalan. Jadi, jangan teragak-agak untuk mengotorkan tangan anda dan bereksperimen dengan set data dan nilai rawak yang berbeza. Dunia sains data adalah tiram anda. Selamat mengekod!