Cum să normalizați matricele NumPy: un ghid rapid

Dacă ați lucrat cu Python pentru analiza datelor sau învățarea automată, probabil că ați întâlnit matrice NumPy. Sunt un instrument puternic pentru manipularea datelor numerice, dar uneori, datele din aceste matrice trebuie să fie ajustate sau „normalizate” pentru a fi utilizate eficient în algoritmii dvs. Dar ce înseamnă normalizarea unei matrice?

Pentru a normaliza o matrice NumPy, trebuie să ajustați valorile din matrice astfel încât să se încadreze într-un anumit interval, de obicei între 0 și 1, sau astfel încât să aibă o distribuție normală standard cu o medie de 0 și o abatere standard de 1 Acest lucru se face adesea în domeniul învățării automate și al analizei datelor pentru a se asigura că toate caracteristicile de intrare au aceeași scară.

În acest articol, vom explora modul în care puteți normaliza o matrice NumPy în Python. Vom analiza diferitele metode pe care le puteți utiliza pentru a normaliza o matrice NumPy și, de asemenea, vom analiza exemple pentru a vă ajuta să înțelegeți mai bine conceptul.

Să intrăm în ea!

Cuprins

• Care sunt elementele de bază ale normalizării în Python?
  • Ce este normalizarea?
  • De ce este importantă normalizarea?
  • Ce sunt normele?
  • Ce este normalizarea în învățarea automată?
• Care sunt tehnicile de normalizare în Python?
  • 1. Cum se efectuează scalarea min-max
  • 2. Cum se efectuează normalizarea L1
  • 3. Cum se efectuează normalizarea L2
• Cum să utilizați Scikit-Learn pentru normalizare în Python
  • 1. Cum să normalizați matricea folosind MinMaxScaler
  • 2. Cum se efectuează normalizarea rândurilor în loc
• Gânduri finale

Care sunt elementele de bază ale normalizării în Python?

Înainte de a implementa normalizarea în Python, trebuie să înțelegeți ce înseamnă normalizarea.

Prin urmare, în această secțiune, vom trece peste ceea ce este normalizarea și conceptele sale de bază.

Ce este normalizarea?

Normalizarea este un proces care scalează și transformă datele într-un interval standardizat. Acest lucru se face prin împărțirea fiecărui element al datelor la un parametru. Parametrul poate fi valoarea maximă, intervalul sau o altă normă.

Puteți normaliza matricea NumPy folosind norma euclidiană (cunoscută și ca norma L2). În plus, puteți, de asemenea, să normalizați tablourile NumPy prin rescalarea valorilor între un anumit interval, de obicei de la 0 la 1.

În Python, biblioteca NumPy oferă o modalitate eficientă de a normaliza tablourile. Aceasta include și matrice și matrice multidimensionale.

De ce este importantă normalizarea?

Normalizarea este importantă, deoarece asigură că diferitele caracteristici sunt tratate în mod egal atunci când se compară și se analizează datele. Puteți să-l utilizați pentru a elimina potențialele părtiniri sau discrepanțe care ar putea apărea din cauza diferitelor scale.

Ce sunt normele?

Parametrul pe care îl utilizați pentru normalizare poate fi norme diferite , cum ar fi norma euclidiană (L2), norma Manhattan (L1) sau norma maximă (L_inf). Folosiți norme pentru a calcula mărimea unui vector sau a unei matrice . Acestea sunt apoi utilizate ca factor de scalare pentru a normaliza datele.

Când lucrăm cu matrici, folosim adesea norma Frobenius , care este o generalizare a normei euclidiene pentru tablourile multidimensionale.

Următorul exemplu arată normalizarea unei matrice folosind norma Frobenius:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
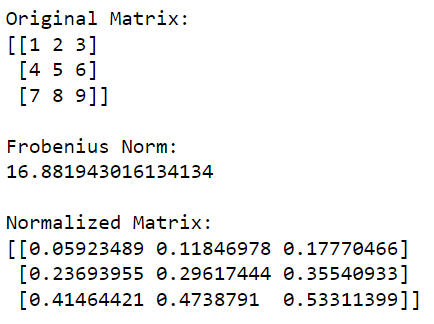
print(normalized_matrix)

Acest cod Python va importa mai întâi biblioteca NumPy și o va folosi pentru a crea o matrice. Apoi calculează norma Frobenius a matricei și apoi împarte fiecare element din matrice la această valoare pentru ao normaliza.

Rezultatul acestui cod este prezentat mai jos:

Ce este normalizarea în învățarea automată?

În învățarea automată , normalizarea este un pas important de preprocesare, deoarece îmbunătățește performanța algoritmilor.

Când efectuați tehnici de optimizare bazate pe gradient, veți descoperi că caracteristicile optimizate tind să convergă mai rapid și mai eficient. Acest lucru se datorează faptului că reduce riscul de scalare slabă sau de dispariție a gradienților.

Care sunt tehnicile de normalizare în Python?

Puteți efectua normalizarea tablourilor NumPy în mai multe moduri. Cu toate acestea, unele metode sunt mai populare decât altele datorită eficienței lor ridicate.

Pentru această secțiune, vom analiza cele trei tehnici de normalizare utilizate pe scară largă:

1. Scalare min-max

2. L1 Normalizare

3. L2 Normalizare

1. Cum se efectuează scalarea min-max

Scalare min-max este cunoscută și ca normalizare liniară sau scalare a caracteristicilor. În scalarea min-max, scalam valorile unui tablou NumPy astfel încât acestea să se încadreze într-un interval specificat, de obicei între 0 și 1.

Pentru a face acest lucru, scadeți valoarea minimă din fiecare element și împărțiți rezultatul la diferența dintre valorile maxime și minime.

Puteți reprezenta scalarea min-max matematic ca:

x' = (x - min(x)) / (max(x) - min(x))

Următorul exemplu demonstrează cum puteți efectua scalarea min-max folosind biblioteca NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Acest cod va importa mai întâi NumPy și apoi va calcula valorile minime și maxime din matrice, pe care apoi le va scala astfel încât toate valorile să fie între 0 (corespunzător valorii minime inițiale) și 1 (corespunzând valorii maxime inițiale).

Rezultatul acestui cod este prezentat mai jos:

Scalare min-max este o formă foarte comună de scalare în învățarea automată și preprocesarea datelor.

2. Cum se efectuează normalizarea L1

Normalizarea L1 folosește norma L1, care este suma valorilor absolute ale elementelor matricei. Acest lucru este util în special pentru matricele rare. Se asigură că suma valorilor absolute ale elementelor matricei normalizate este egală cu 1.

Formula pentru normalizarea L1 este:

x' = x / sum(|x|)

Următorul exemplu arată cum puteți efectua normalizarea L1 folosind NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
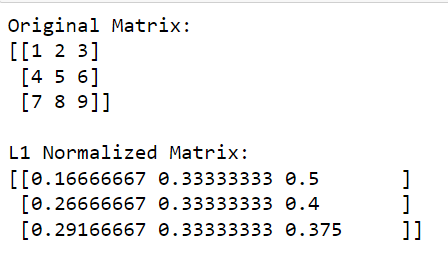
print('nL1 Normalized Matrix:')
print(l1_normalized_matrix)

În acest cod, np.linalg.norm (matrice, 1, axa=1, keepdims=True) calculează norma L1 pentru fiecare rând (acest lucru se face prin specificarea axei=1).

Această operație va returna un vector coloană în care fiecare element este norma L1 a rândului corespunzător. Prin împărțirea matricei inițiale la aceste norme (efectuând diviziunea element-wire), obținem versiunea normalizată L1 a matricei.

Rezultatul este dat mai jos:

3. Cum se efectuează normalizarea L2

Normalizarea L2 folosește norma L2, care este rădăcina pătrată a sumei elementelor matricei pătrate.

Această metodă convertește tabloul normalizat într-un vector unitar cu o normă 2 de 1. Normalizarea L2 este utilă pentru reducerea dimensională și asigură o importanță egală pentru toate caracteristicile.

Formula pentru normalizarea L2 este:

x' = x / sqrt(sum(x^2))

Iată cum puteți efectua normalizarea L2 folosind NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
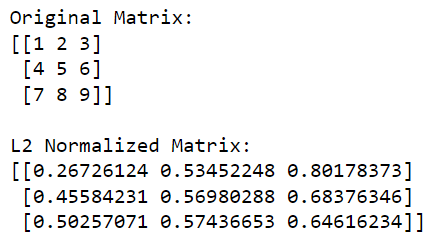
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

În acest cod, np.linalg.norm(matrix, 2, axis=1, keepdims=True) calculează norma L2 (norma euclidiană) pentru fiecare rând (acest lucru se face prin specificarea axei=1). Această operație va returna un vector coloană în care fiecare element este norma L2 a rândului corespunzător.

Împărțind matricea inițială la aceste norme (efectuând diviziunea element-wire), obținem versiunea normalizată L2 a matricei.

Rezultatul este dat mai jos:

Bine, acum că am trecut peste modalitățile populare de a crea o matrice normalizată folosind NumPy, să aruncăm o privire la modul în care puteți face același lucru folosind alte biblioteci Python în secțiunea următoare.

Cum să utilizați Scikit-Learn pentru normalizare în Python

Scikit-learn este o bibliotecă Python puternică pentru învățarea automată. Acesta oferă mai multe instrumente pentru preprocesarea datelor.

Un instrument pe care îl puteți utiliza este modulul sklearn.preprocessing , care oferă diverse tehnici pentru a efectua normalizarea. Există multe funcții de scalare, transformatoare și normalizatoare diferite disponibile. Cu toate acestea, ne vom concentra pe MinMaxScaler și pe funcția de normalizare .

Pentru a preprocesa datele cu scikit-learn, utilizați în principal API-ul transformer. Aceasta include metodele fit , transform și fit_transform .

1. Cum să normalizați matricea folosind MinMaxScaler

MinMaxScaler este un scaler care normalizează datele într- un interval specificat, de obicei [0, 1].

Formula pentru MinMaxScalar este dată mai jos:

scaled_value = (value - min_value) / (max_value - min_value)

Pentru a implementa MinMaxScaler , puteți urma acești pași:

1. Importați bibliotecile necesare:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Creați o matrice NumPy:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Instanțiați MinMaxScaler și potriviți-l la date:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Transformați datele folosind metoda transform sau fit_transform :

   normalized_data = scaler.transform(data)

Rezultatul acestui cod este prezentat mai jos:

După cum puteți vedea în rezultat, MinMaxScalarMatrix are doar valori cuprinse între 0 și 1.

2. Cum se efectuează normalizarea rândurilor în loc

De asemenea, puteți utiliza normalizarea rândurilor la loc ca alternativă, folosind funcția de normalizare .

Această metodă normalizează fiecare matrice de intrare sau caracteristică independent prin scalarea vectorului la o normă de unitate. În mod implicit, funcția de normalizare utilizează norma L2 pentru a efectua o normalizare simplă, dar puteți alege alte opțiuni de normă.

Următorul exemplu demonstrează normalizarea rândurilor pe loc:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

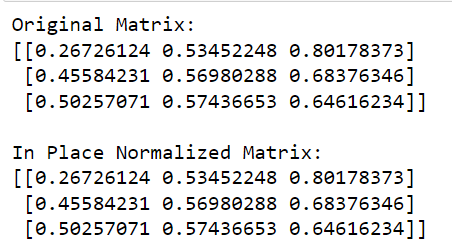
print('L2 Normalized Matrix:')
print(matrix)

În acest cod, numim funcția normalize din sklearn , definim norma de utilizat ('l2' în acest caz) și setăm copy=False pentru a efectua normalizarea pe loc.

Rezultatul acestui cod este prezentat mai jos:

Pentru a afla mai multe despre învățarea automată în Python , vedeți următorul videoclip:

Gânduri finale

Pe măsură ce explorați în continuare știința datelor și învățarea automată, veți descoperi că procesul de normalizare este un pas esențial în conducta dvs. de preprocesare a datelor.

În primul rând, plasează diferite caracteristici pe o scară comună. Acest lucru face ca modelele dvs. să fie mai puțin sensibile la scara intrărilor. Poate îmbunătăți considerabil performanța multor algoritmi de învățare automată.

În al doilea rând, vă ajută să accelerați procesul de antrenament. Unii algoritmi, în special cei bazați pe calcule ale distanțelor calculate, converg mai repede atunci când datele sunt normalizate.

Învățând cum să normalizați datele, vă echipați cu o abilitate crucială. Normalizarea este un instrument practic folosit în mod curent în aplicațiile din lumea reală. Vă va ajuta să reduceți probabilitatea unor rezultate neașteptate din cauza valorii aberante sau a diferențelor de unități.

Ca orice instrument, cheia stăpânirii normalizării constă în practică. Deci, nu ezitați să vă murdăriți mâinile și să experimentați cu diferite seturi de date și valori aleatorii. Lumea științei datelor este stridia ta. Codare fericită!