Hoe NumPy-arrays te normaliseren: een beknopte handleiding

Als je met Python hebt gewerkt voor data-analyse of machine learning, ben je waarschijnlijk NumPy-arrays tegengekomen. Ze zijn een krachtig hulpmiddel voor het verwerken van numerieke gegevens, maar soms moeten de gegevens binnen deze arrays worden aangepast of 'genormaliseerd' om effectief in uw algoritmen te kunnen worden gebruikt. Maar wat betekent het om een ​​array te normaliseren?

Om een ​​NumPy-array te normaliseren, moet u de waarden in de array aanpassen zodat ze binnen een bepaald bereik vallen, meestal tussen 0 en 1, of zodat ze een standaardnormale verdeling hebben met een gemiddelde van 0 en een standaarddeviatie van 1 Dit wordt vaak gedaan op het gebied van machine learning en data-analyse om ervoor te zorgen dat alle invoerfuncties dezelfde schaal hebben.

In dit artikel zullen we onderzoeken hoe u een NumPy-array in Python kunt normaliseren. We bekijken de verschillende methoden die u kunt gebruiken om een ​​NumPy-array te normaliseren en kijken ook naar voorbeelden om u te helpen het concept beter te begrijpen.

Laten we erop ingaan!

Inhoudsopgave

• Wat zijn de basisprincipes van normalisatie in Python?
  • Wat is normalisatie?
  • Waarom is normalisatie belangrijk?
  • Wat zijn normen?
  • Wat is normalisatie bij machine learning?
• Wat zijn de normalisatietechnieken in Python?
  • 1. Hoe min-max-schaling uit te voeren
  • 2. Hoe L1-normalisatie uit te voeren
  • 3. Hoe L2-normalisatie uit te voeren
• Scikit-Learn gebruiken voor normalisatie in Python
  • 1. Array normaliseren met MinMaxScaler
  • 2. Hoe in-place rijnormalisatie uit te voeren
• Laatste gedachten

Wat zijn de basisprincipes van normalisatie in Python?

Voordat we normalisatie in Python implementeren, moet u begrijpen wat normalisatie betekent.

Daarom gaan we in dit gedeelte in op wat normalisatie is en wat de kernconcepten ervan zijn.

Wat is normalisatie?

Normalisatie is een proces dat gegevens schaalt en omzet in een gestandaardiseerd bereik. Dit wordt gedaan door elk element van de gegevens te delen door een parameter. De parameter kan de maximumwaarde, het bereik of een andere norm zijn.

U kunt de NumPy-array normaliseren met behulp van de Euclidische norm (ook bekend als de L2-norm). Bovendien kunt u NumPy-arrays ook normaliseren door de waarden opnieuw te schalen tussen een bepaald bereik, meestal 0 tot 1.

In Python biedt de NumPy-bibliotheek een efficiënte manier om arrays te normaliseren. Dit omvat ook multidimensionale arrays en matrices.

Waarom is normalisatie belangrijk?

Normalisatie is belangrijk omdat het ervoor zorgt dat verschillende kenmerken gelijk worden behandeld bij het vergelijken en analyseren van gegevens. U kunt het gebruiken om mogelijke vooroordelen of discrepanties te elimineren die kunnen ontstaan ​​als gevolg van verschillende schalen.

Wat zijn normen?

De parameter die u voor normalisatie gebruikt, kunnen verschillende normen zijn , zoals de Euclidische norm (L2), de Manhattan-norm (L1) of de max-norm (L_inf). Je gebruikt normen om de grootte van een vector of matrix te berekenen . Deze worden vervolgens gebruikt als schaalfactor om de gegevens te normaliseren.

Bij het werken met matrices gebruiken we vaak de Frobenius-norm , wat een veralgemening is van de Euclidische norm voor meerdimensionale arrays.

Het volgende voorbeeld toont de normalisatie van een matrix met behulp van de Frobenius-norm:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
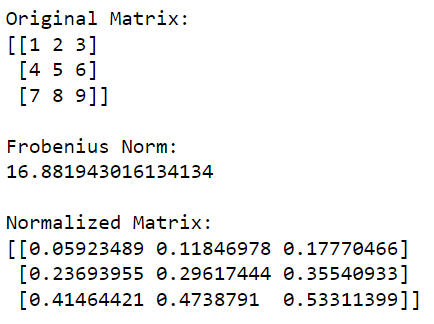
print(normalized_matrix)

Deze Python-code importeert eerst de NumPy-bibliotheek en gebruikt deze om een ​​matrix te maken. Vervolgens berekent het de Frobenius-norm van de matrix en deelt vervolgens elk element in de matrix door deze waarde om het te normaliseren.

De uitvoer van deze code wordt hieronder weergegeven:

Wat is normalisatie bij machine learning?

Bij machine learning is normalisatie een belangrijke voorbewerkingsstap omdat het de prestaties van algoritmen verbetert.

Bij het uitvoeren van op gradiënt gebaseerde optimalisatietechnieken, zult u merken dat geoptimaliseerde functies sneller en efficiënter convergeren. Dit komt omdat het risico op slecht schalen of verdwijnende hellingen wordt verkleind.

Wat zijn de normalisatietechnieken in Python?

U kunt op een aantal manieren normalisatie van NumPy- arrays uitvoeren. Sommige methoden zijn echter populairder dan andere vanwege hun hoge efficiëntie.

Voor deze sectie zullen we kijken naar de drie veelgebruikte normalisatietechnieken:

1. Min-Max Schaling

2. L1 Normalisatie

3. L2 Normalisatie

1. Hoe min-max-schaling uit te voeren

Min-max-schaling wordt ook wel lineaire normalisatie of feature-scaling genoemd. Bij min-max-schaling schalen we de waarden van een NumPy-array zodat ze binnen een opgegeven bereik vallen, meestal tussen 0 en 1.

Om dit te doen, trekt u de minimumwaarde van elk element af en deelt u het resultaat door het verschil tussen de maximum- en minimumwaarden.

U kunt de min-max-schaling wiskundig weergeven als:

x' = (x - min(x)) / (max(x) - min(x))

Het volgende voorbeeld laat zien hoe u min-max schaling kunt uitvoeren met behulp van de NumPy-bibliotheek:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Deze code importeert eerst NumPy en berekent vervolgens de minimum- en maximumwaarden in de matrix, die vervolgens zodanig wordt geschaald dat alle waarden tussen 0 (overeenkomend met de oorspronkelijke minimumwaarde) en 1 (overeenkomend met de oorspronkelijke maximumwaarde) liggen.

De uitvoer van deze code wordt hieronder weergegeven:

Min-max-schaling is een veel voorkomende vorm van schaling bij machine learning en gegevensvoorverwerking.

2. Hoe L1-normalisatie uit te voeren

L1-normalisatie maakt gebruik van de L1-norm, die de som is van de absolute waarden van de array-elementen. Dit is vooral handig voor schaarse matrices. Het zorgt ervoor dat de som van de absolute waarden van de genormaliseerde array-elementen gelijk is aan 1.

De formule voor L1-normalisatie is:

x' = x / sum(|x|)

Het volgende voorbeeld laat zien hoe u L1-normalisatie kunt uitvoeren met behulp van NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
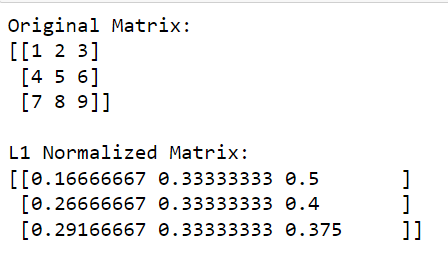
print(l1_normalized_matrix)

In deze code berekent np.linalg.norm (matrix, 1, axis=1, keepdims=True) de L1-norm voor elke rij (dit wordt gedaan door as=1 op te geven).

Deze bewerking retourneert een kolomvector waarin elk element de L1-norm is van de overeenkomstige rij. Door de originele matrix te delen door deze normen (de deling elementsgewijs uitvoeren), verkrijgen we de L1 genormaliseerde versie van de matrix.

De uitvoer wordt hieronder gegeven:

3. Hoe L2-normalisatie uit te voeren

L2-normalisatie gebruikt de L2-norm, die de vierkantswortel is van de som van de gekwadrateerde array-elementen.

Deze methode zet de genormaliseerde array om in een eenheidsvector met een 2-norm van 1. L2-normalisatie is nuttig voor dimensionale reductie en zorgt ervoor dat alle kenmerken even belangrijk zijn.

De formule voor L2-normalisatie is:

x' = x / sqrt(sum(x^2))

Dit is hoe u L2-normalisatie kunt uitvoeren met behulp van NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
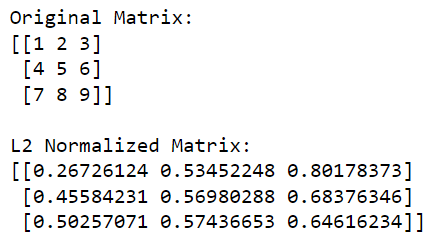
print(l2_normalized_matrix)

In deze code berekent np.linalg.norm(matrix, 2, axis=1, keepdims=True) de L2-norm (Euclidische norm) voor elke rij (dit wordt gedaan door as=1 op te geven). Deze bewerking retourneert een kolomvector waarin elk element de L2-norm is van de overeenkomstige rij.

Door de oorspronkelijke matrix te delen door deze normen (de deling elementsgewijs uitvoeren), verkrijgen we de L2 genormaliseerde versie van de matrix.

De uitvoer wordt hieronder gegeven:

Oké, nu we de populaire manieren hebben besproken om een ​​genormaliseerde array te maken met behulp van NumPy, laten we in de volgende sectie eens kijken hoe je hetzelfde kunt doen met andere Python-bibliotheken.

Scikit-Learn gebruiken voor normalisatie in Python

Scikit-learn is een krachtige Python-bibliotheek voor machine learning. Het biedt verschillende hulpmiddelen voor het voorbewerken van gegevens.

Een hulpmiddel dat u kunt gebruiken, is de module sklearn.preprocessing , die verschillende technieken biedt om normalisatie uit te voeren. Er zijn veel verschillende scaler-functies, transformatoren en normalizers beschikbaar. We zullen ons echter concentreren op MinMaxScaler en de functie normaliseren .

Voor het voorbewerken van data met scikit-learn gebruik je voornamelijk de transformer API. Dit omvat de methoden fit , transform en fit_transform .

1. Array normaliseren met MinMaxScaler

De MinMaxScaler is een scaler die gegevens normaliseert tot een bepaald bereik, meestal [0, 1].

De formule voor MinMaxScalar wordt hieronder gegeven:

scaled_value = (value - min_value) / (max_value - min_value)

Om de MinMaxScaler te implementeren , kunt u deze stappen volgen:

1. Importeer de vereiste bibliotheken:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Maak een NumPy-array:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Instantiseer de MinMaxScaler en pas deze aan de gegevens aan:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Transformeer de gegevens met behulp van de methode transform of fit_transform :

   normalized_data = scaler.transform(data)

De uitvoer van deze code wordt hieronder weergegeven:

Zoals je in de uitvoer kunt zien, heeft de MinMaxScalarMatrix alleen waarden van 0 tot 1.

2. Hoe in-place rijnormalisatie uit te voeren

U kunt ook de in-place rijnormalisatie gebruiken als alternatief, met behulp van de functie normaliseren .

Deze methode normaliseert elke invoerarray of functie onafhankelijk door de vector te schalen naar een eenheidsnorm. Standaard gebruikt de normalisatiefunctie de L2-norm om eenvoudige normalisatie uit te voeren, maar u kunt andere normopties kiezen.

Het volgende voorbeeld demonstreert in-place rijnormalisatie:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
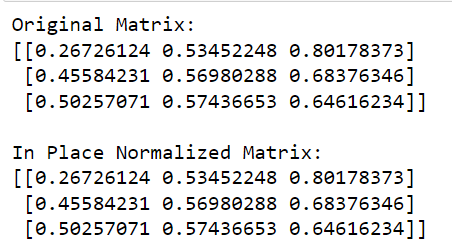
print(matrix)

In deze code noemen we de functie normalize van sklearn , definiëren we de te gebruiken norm (in dit geval 'l2') en stellen we copy=False in om interne normalisatie uit te voeren.

De uitvoer van deze code wordt hieronder weergegeven:

Bekijk de volgende video voor meer informatie over machine learning in Python :

Laatste gedachten

Naarmate u meer onderzoek doet naar datawetenschap en machine learning, zult u merken dat het normalisatieproces een essentiële stap is in uw datavoorverwerkingspijplijn.

Ten eerste plaatst het verschillende kenmerken op een gemeenschappelijke schaal. Dit maakt uw modellen minder gevoelig voor de schaal van invoer. Het kan de prestaties van veel algoritmen voor machine learning aanzienlijk verbeteren.

Ten tweede helpt het u bij het versnellen van het trainingsproces. Sommige algoritmen, vooral die gebaseerd op berekende afstandsberekeningen, convergeren sneller wanneer gegevens worden genormaliseerd.

Door te leren hoe u gegevens kunt normaliseren, rust u uzelf uit met een cruciale vaardigheid. Normalisatie is een praktisch hulpmiddel dat routinematig wordt gebruikt in real-world toepassingen. Het zal u helpen bij het verkleinen van de kans op onverwachte resultaten als gevolg van uitschieters of verschillen in eenheden.

Zoals bij elk hulpmiddel ligt de sleutel tot het beheersen van normalisatie in de praktijk. Aarzel dus niet om je handen vuil te maken en te experimenteren met verschillende datasets en willekeurige waarden. De wereld van data science ligt aan je voeten. Veel codeerplezier!