Como normalizar matrizes NumPy: um guia rápido

Se você trabalha com Python para análise de dados ou aprendizado de máquina, provavelmente já se deparou com arrays NumPy. Eles são uma ferramenta poderosa para lidar com dados numéricos, mas, às vezes, os dados dentro dessas matrizes precisam ser ajustados ou 'normalizados' para serem usados ​​com eficácia em seus algoritmos. Mas o que significa normalizar um array?

Para normalizar uma matriz NumPy, você deve ajustar os valores na matriz para que caiam dentro de um determinado intervalo, normalmente entre 0 e 1, ou para que tenham uma distribuição normal padrão com média 0 e desvio padrão 1 Isso geralmente é feito no campo de aprendizado de máquina e análise de dados para garantir que todos os recursos de entrada tenham a mesma escala.

Neste artigo, exploraremos como você pode normalizar um array NumPy em Python. Veremos os diferentes métodos que você pode usar para normalizar um array NumPy e também veremos exemplos para ajudá-lo a entender melhor o conceito.

Vamos entrar nisso!

Índice

• Quais são os fundamentos da normalização em Python?
  • O que é Normalização?
  • Por que a normalização é importante?
  • O que são normas?
  • O que é normalização no aprendizado de máquina?
• Quais são as técnicas de normalização em Python?
  • 1. Como executar o escalonamento mínimo-máximo
  • 2. Como realizar a normalização L1
  • 3. Como executar a normalização L2
• Como usar o Scikit-Learn para normalização em Python
  • 1. Como normalizar array usando MinMaxScaler
  • 2. Como executar a normalização de linha no local
• Pensamentos finais

Quais são os fundamentos da normalização em Python?

Antes de implementarmos a normalização no Python, você deve entender o que significa normalização.

Portanto, nesta seção, veremos o que é normalização e seus principais conceitos.

O que é Normalização?

A normalização é um processo que dimensiona e transforma dados em um intervalo padronizado. Isso é feito dividindo cada elemento dos dados por um parâmetro. O parâmetro pode ser o valor máximo, faixa ou alguma outra norma.

Você pode normalizar a matriz NumPy usando a norma euclidiana (também conhecida como norma L2). Além disso, você também pode normalizar as matrizes NumPy redimensionando os valores entre um determinado intervalo, geralmente de 0 a 1.

Em Python, a biblioteca NumPy fornece uma maneira eficiente de normalizar arrays. Isso inclui arrays e matrizes multidimensionais também.

Por que a normalização é importante?

A normalização é importante, pois garante que diferentes recursos sejam tratados igualmente ao comparar e analisar dados. Você pode usá-lo para eliminar possíveis vieses ou discrepâncias que possam surgir devido a escalas variáveis.

O que são normas?

O parâmetro que você usa para normalização pode ser normas diferentes , como a norma euclidiana (L2), a norma de Manhattan (L1) ou a norma máxima (L_inf). Você usa normas para calcular a magnitude de um vetor ou matriz . Estes são então usados ​​como um fator de escala para normalizar os dados.

Ao trabalhar com matrizes, geralmente usamos a norma de Frobenius , que é uma generalização da norma euclidiana para matrizes multidimensionais.

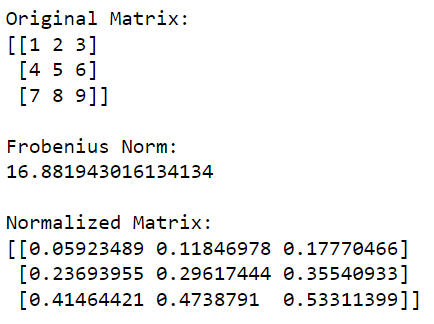
O exemplo a seguir mostra a normalização de uma matriz usando a norma de Frobenius:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
print(normalized_matrix)

Este código Python primeiro importará a biblioteca NumPy e a usará para criar uma matriz. Em seguida, ele calcula a norma Frobenius da matriz e divide cada elemento na matriz por esse valor para normalizá-lo.

A saída deste código é dada abaixo:

O que é normalização no aprendizado de máquina?

No aprendizado de máquina , a normalização é uma importante etapa de pré-processamento, pois melhora o desempenho dos algoritmos.

Ao executar técnicas de otimização baseadas em gradiente, você descobrirá que os recursos otimizados tendem a convergir de forma mais rápida e eficiente. Isso ocorre porque reduz o risco de escalonamento ruim ou gradientes que desaparecem.

Quais são as técnicas de normalização em Python?

Você pode executar a normalização de matrizes NumPy de várias maneiras. No entanto, alguns métodos são mais populares do que outros devido à sua alta eficiência.

Nesta seção, veremos as três técnicas de normalização amplamente usadas:

1. Escala Mín-Máx

2. Normalização L1

3. Normalização L2

1. Como executar o escalonamento mínimo-máximo

O dimensionamento mínimo-máximo também é conhecido como normalização linear ou dimensionamento de recursos. Na escala min-max, escalamos os valores de uma matriz NumPy para que caiam dentro de um intervalo especificado, geralmente entre 0 e 1.

Para fazer isso, você subtrai o valor mínimo de cada elemento e divide o resultado pela diferença entre os valores máximo e mínimo.

Você pode representar a escala min-max matematicamente como:

x' = (x - min(x)) / (max(x) - min(x))

O exemplo a seguir demonstra como você pode executar a escala min-max usando a biblioteca NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Esse código primeiro importará NumPy e, em seguida, calculará os valores mínimo e máximo na matriz, que serão dimensionados de modo que todos os valores estejam entre 0 (correspondente ao valor mínimo original) e 1 (correspondente ao valor máximo original).

A saída deste código é dada abaixo:

O dimensionamento mínimo-máximo é uma forma muito comum de dimensionamento em aprendizado de máquina e pré-processamento de dados.

2. Como realizar a normalização L1

A normalização L1 emprega a norma L1, que é a soma dos valores absolutos dos elementos da matriz. Isso é particularmente útil para matrizes esparsas. Ele garante que a soma dos valores absolutos dos elementos da matriz normalizada seja igual a 1.

A fórmula para a normalização L1 é:

x' = x / sum(|x|)

O exemplo a seguir mostra como você pode executar a normalização L1 usando NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
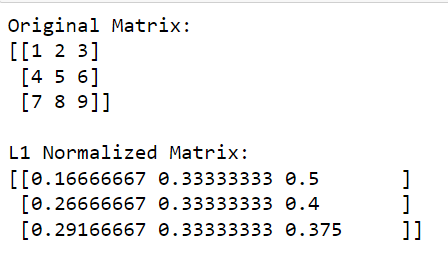
print(l1_normalized_matrix)

Nesse código, np.linalg.norm (matriz, 1, eixo=1, keepdims=True) calcula a norma L1 para cada linha (isso é feito especificando eixo=1).

Esta operação retornará um vetor coluna onde cada elemento é a norma L1 da linha correspondente. Dividindo a matriz original por essas normas (realizando a divisão elemento a elemento), obtemos a versão normalizada L1 da matriz.

A saída é dada abaixo:

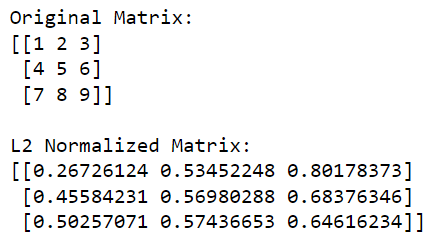
3. Como executar a normalização L2

A normalização L2 usa a norma L2, que é a raiz quadrada da soma dos elementos quadrados da matriz.

Este método converte a matriz normalizada em um vetor unitário com uma norma 2 de 1. A normalização L2 é útil para redução dimensional e garante igual importância para todos os recursos.

A fórmula para a normalização L2 é:

x' = x / sqrt(sum(x^2))

É assim que você pode executar a normalização L2 usando NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

Neste código, np.linalg.norm(matriz, 2, eixo=1, keepdims=True) calcula a norma L2 (norma euclidiana) para cada linha (isso é feito especificando eixo=1). Esta operação retornará um vetor coluna onde cada elemento é a norma L2 da linha correspondente.

Ao dividir a matriz original por essas normas (realizando a divisão elemento a elemento), obtemos a versão normalizada L2 da matriz.

A saída é dada abaixo:

Tudo bem, agora que examinamos as formas populares de criar uma matriz normalizada usando NumPy, vamos dar uma olhada em como você pode fazer o mesmo usando outras bibliotecas Python na próxima seção.

Como usar o Scikit-Learn para normalização em Python

Scikit-learn é uma poderosa biblioteca Python para aprendizado de máquina. Ele fornece várias ferramentas para pré-processamento de dados.

Uma ferramenta que você pode usar é o módulo sklearn.preprocessing , que oferece várias técnicas para executar a normalização. Existem muitas funções diferentes de escalador, transformadores e normalizadores disponíveis. No entanto, vamos nos concentrar no MinMaxScaler e na função normalizar .

Para pré-processar dados com o scikit-learn, você usa principalmente a API do transformador. Isso inclui os métodos fit , transform e fit_transform .

1. Como normalizar array usando MinMaxScaler

O MinMaxScaler é um scaler que normaliza os dados para um intervalo especificado, geralmente [0, 1].

A fórmula para MinMaxScalar é dada abaixo:

scaled_value = (value - min_value) / (max_value - min_value)

Para implementar o MinMaxScaler , você pode seguir estas etapas:

1. Importe as bibliotecas necessárias:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Crie uma matriz NumPy:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Instancie o MinMaxScaler e ajuste-o aos dados:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Transforme os dados usando o método transform ou fit_transform :

   normalized_data = scaler.transform(data)

A saída deste código é dada abaixo:

Como você pode ver na saída, MinMaxScalarMatrix possui apenas valores que variam de 0 a 1.

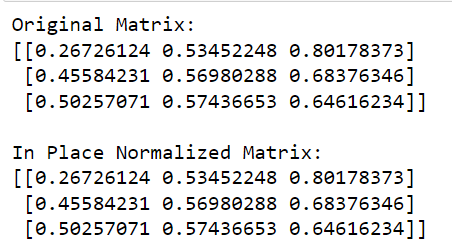
2. Como executar a normalização de linha no local

Você também pode usar a normalização de linha no local como alternativa, usando a função normalizar .

Esse método normaliza cada matriz de entrada ou recurso independentemente, dimensionando o vetor para uma norma de unidade. Por padrão, a função normalizar usa a norma L2 para realizar normalização simples, mas você pode escolher outras opções de norma.

O exemplo a seguir demonstra a normalização de linha no local:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
print(matrix)

Neste código, chamamos a função normalize de sklearn , definimos a norma a ser usada ('l2' neste caso) e definimos copy=False para executar a normalização no local.

A saída deste código é dada abaixo:

Para saber mais sobre aprendizado de máquina em Python , confira o seguinte vídeo:

Pensamentos finais

À medida que você explora mais a ciência de dados e o aprendizado de máquina, descobrirá que o processo de normalização é uma etapa essencial em seu pipeline de pré-processamento de dados.

Em primeiro lugar, coloca diferentes características em uma escala comum. Isso torna seus modelos menos sensíveis à escala de entradas. Ele pode melhorar muito o desempenho de muitos algoritmos de aprendizado de máquina.

Em segundo lugar, ajuda você a acelerar o processo de treinamento. Alguns algoritmos, especialmente aqueles baseados em cálculos de distância calculada, convergem mais rapidamente quando os dados são normalizados.

Ao aprender a normalizar dados, você se equipara com uma habilidade crucial. A normalização é uma ferramenta prática usada rotineiramente em aplicações do mundo real. Isso o ajudará a reduzir a probabilidade de resultados inesperados devido a discrepâncias ou diferenças nas unidades.

Como qualquer ferramenta, a chave para dominar a normalização está na prática. Portanto, não hesite em colocar a mão na massa e experimentar diferentes conjuntos de dados e valores aleatórios. O mundo da ciência de dados é sua ostra. Codificação feliz!