So verwenden Sie Chi-Quadrat-Verteilungen in Excel

Einige statistische Maße in Excel können sehr verwirrend sein, aber Chi-Quadrat-Funktionen sind wirklich praktisch. Auch wenn Sie nur eine der Chi-Quadrat-Funktionen verwenden, lesen Sie sich alle drei Funktionsbeschreibungen durch. Als eine Reihe von statistischen Werkzeugen betrachtet, machen die Funktionen einiges mehr Sinn.

CHISQ.DIST.RT: Chi-Quadrat-Verteilung

Die Funktion CHISQ.DIST.RT, die die rechtsseitige Wahrscheinlichkeit einer Chi-Quadrat-Verteilung berechnet, berechnet ein Signifikanzniveau unter Verwendung des Chi-Quadrat-Werts und der Freiheitsgrade. Der Chi-Quadrat-Wert entspricht der Summe der quadrierten standardisierten Werte. Die Funktion verwendet die Syntax

=CHISQ.VERT.RT( x , deg_freedom )

wobei x dem Chi-Quadrat-Wert und deg_freedom den Freiheitsgraden entspricht.

Als Beispiel dafür, wie all das funktioniert, nehmen Sie an, Sie sind mehr als ein bisschen misstrauisch gegenüber einem Spielautomaten, der eines von sechs Bildern zeigt: Diamanten, Sterne, Cowboystiefel, Kirschen, Orangen oder Goldtöpfe. Bei sechs Möglichkeiten könnten Sie erwarten, dass in einer großen Stichprobe jede der sechs Möglichkeiten etwa in einem Sechstel der Fälle auftaucht.

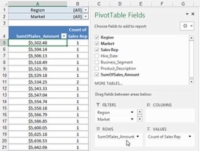
Angenommen, die Stichprobengröße beträgt beispielsweise 180. In diesem Fall könnten Sie erwarten, dass jede Spielautomaten-Möglichkeit 30 Mal vorkommt, da 180/6 gleich 30 ist. Wenn Sie ein Arbeitsblattfragment wie dieses erstellen, könnten Sie den einarmigen Banditen analysieren.

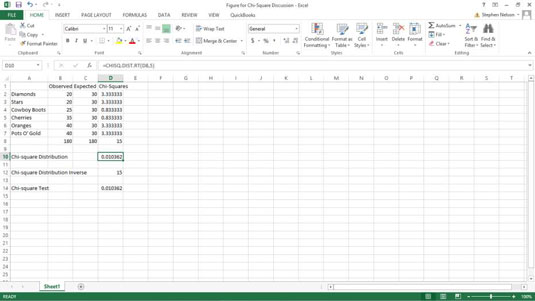
Um das Signifikanzniveau und die Chi-Quadrat-Verteilungsfunktion zu berechnen, könnten Sie die folgende Formel in D10 eingeben:

=CHISQ.DIST.RT(D8,5)

Die Funktion gibt den Wert 0,010362338 zurück. Dies ist die Signifikanzstufe, die ein Chi-Quadrat-Wert von 15 auf einen Stichprobenfehler zurückzuführen ist.

Zelle D8 enthält den Chi-Quadrat-Wert, der einfach die Summe der quadrierten Differenzen zwischen den beobachteten und den erwarteten Werten ist. Der Wert in Zelle D2 wird beispielsweise mit der Formel =+(B2–C2)^2/C2 berechnet, um den Wert 3.333333333 zurückzugeben. Voraussichtlich berechnen ähnliche Formeln im Bereich D3:D7 die quadrierten Differenzen für die anderen Spielautomatensymbole. Übrigens lautet die Formel in Zelle D8 =SUMME(D2:D7).

Fazit: Es sieht nicht gut aus, oder? Es besteht nur eine 1-Prozent-Chance, dass der Spielautomat, um den Sie sich Sorgen machen, tatsächlich die beobachteten Werte zufällig produzieren könnte. Sehr verdächtig.

CHISQ.DIST: Chi-Quadrat-Verteilung

Die Funktion CHISQ.VERT ähnelt der Funktion CHISQ.VERT.RT, berechnet jedoch die linksseitige Wahrscheinlichkeit einer Chi-Quadrat-Verteilung. Die Funktion verwendet die Syntax

=CHISQ.VERT(x,deg_freedom,kumulativ)

wobei x dem Chi-Quadrat-Wert entspricht, deg_freedom den Freiheitsgraden entspricht und kumulativ ein Schalter ist, den Sie auf 0 oder FALSE setzen, wenn Sie eine Wahrscheinlichkeitsdichte berechnen möchten, und auf 1 oder TRUE, wenn Sie eine kumulative Wahrscheinlichkeit berechnen möchten.

CHISQ.INV.RT: Rechtseitige Chi-Quadrat-Verteilungswahrscheinlichkeit

Die Funktion CHISQ.INV.RT gibt den Kehrwert der rechtsseitigen Wahrscheinlichkeit einer Chi-Quadrat-Verteilung zurück. Die Funktion verwendet die Syntax

=CHISQ.INV.RT(Wahrscheinlichkeit,Grad_Freiheit)

wobei Wahrscheinlichkeit gleich dem Signifikanzniveau und deg_freedom gleich den Freiheitsgraden ist.

Ein Beispiel für die Funktion CHISQ.INV.RT finden Sie im Arbeitsblattfragment. Mit sechs möglichen Ergebnissen am Spielautomaten haben Sie fünf Freiheitsgrade. Wenn Sie also das Chi-Quadrat berechnen möchten, das einem Signifikanzniveau von 0,010362338 entspricht, können Sie die folgende Formel in Zelle D12 eingeben:

=CHISQ.INV.RT(D10,5)

Diese Funktion gibt den Wert 14,99996888 zurück, der ziemlich nahe bei 15 liegt. Beachten Sie, dass D10 als erstes Wahrscheinlichkeitsargument verwendet wird, da diese Zelle das von der Funktion CHISQ.VERT berechnete Signifikanzniveau enthält.

CHISQ.INV: Linksseitige Chi-Quadrat-Verteilungswahrscheinlichkeit

Die Funktion CHISQ.INV gibt die linksseitige Wahrscheinlichkeit einer Chi-Quadrat-Verteilung zurück. Die Funktion verwendet die Syntax

=CHISQ.INV(Wahrscheinlichkeit,Grad_Freiheit)

wobei Wahrscheinlichkeit gleich dem Signifikanzniveau und deg_freedom gleich den Freiheitsgraden ist.

Um den Chi-Quadrat-Wert zu berechnen, der einem Signifikanzniveau von 0,010362338 mit 5 Freiheitsgraden entspricht, könnten Sie die folgende Formel in eine Zelle des Arbeitsblatts eingeben:

=CHISQ.INV(0.010362338,5)

Diese Funktion gibt den Wert .562927 zurück.

CHISQ.TEST: Chi-Quadrat-Test

Mit der Chi-Quadrat-Testfunktion können Sie beurteilen, ob Unterschiede zwischen den beobachteten und den erwarteten Werten Zufall oder Stichprobenfehler darstellen. Die Funktion verwendet die Syntax

=CHISQ.TEST(tatsächlicher_Bereich,erwarteter_Bereich)

Nochmals auf das Beispiel des verdächtigen Spielautomaten Bezug nehmend, könnten Sie einen Chi-Quadrat-Test durchführen, indem Sie die folgende Formel in Zelle D14 eingeben und dann das, was Sie beobachten, mit dem vergleichen, was Sie erwarten:

=CHISQ.TEST(B2:B7,C2:C7)

Die Funktion gibt den in Zelle D14 angezeigten p-Wert oder die Wahrscheinlichkeit zurück, was darauf hinweist, dass nur eine Wahrscheinlichkeit von 1,0362 % besteht, dass die Unterschiede zwischen den beobachteten und erwarteten Ergebnissen auf Stichprobenfehler zurückzuführen sind.

Ein gemeinsames Merkmal eines Chi-Quadrat-Tests ist der Vergleich des p-Werts – wieder der Wert, den die Funktion CHISQ.TEST zurückgibt – mit einem Signifikanzniveau. Im Fall des verdächtigen Spielautomaten könnten Sie beispielsweise sagen: „Weil man nicht 100-prozentig sicher sein kann, sagen wir, dass wir eine Wahrscheinlichkeit von 95 Prozent haben wollen, was einem 5-Prozent-Niveau entspricht Bedeutung."

Wenn der p-Wert unter dem Signifikanzniveau liegt, gehen Sie davon aus, dass etwas faul ist. Statistiker, die nicht so erdig klingen wollen, haben einen anderen Ausdruck für diese etwas faulige Schlussfolgerung: die Nullhypothese abzulehnen.