So verwenden Sie die POISSON.DIST-Funktion von Excel

Poisson kann ein sehr nützliches Werkzeug für die statistische Analyse mit Excel sein. Nicht zeigen, wie es funktioniert? Hier sind die Schritte zur Verwendung von POISSON.DIST von Excel:

Wählen Sie eine Zelle für die Antwort von POISSON.DIST aus.

Wählen Sie im Menü Statistische Funktionen die Option POISSON.VERT aus, um das Dialogfeld Funktionsargumente zu öffnen.

Geben Sie im Dialogfeld Funktionsargumente die entsprechenden Werte für die Argumente ein.
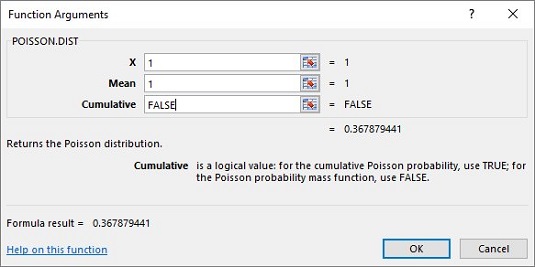
Geben Sie im Feld X die Anzahl der Ereignisse ein, für die Sie die Wahrscheinlichkeit bestimmen. In diesem Beispiel suchen Sie nach pr (1), geben Sie also 1 ein.
Geben Sie im Feld Mittelwert den Mittelwert des Prozesses ein, der in diesem Beispiel 1 ist.
Im Feld Kumulativ ist es entweder WAHR für die kumulative Wahrscheinlichkeit oder FALSE nur für die Wahrscheinlichkeit der Anzahl von Ereignissen. Geben Sie FALSCH ein.
Bei den Einträgen für X, Mittelwert und Kumulativ erscheint die Antwort im Dialogfeld. Die Antwort für dieses Beispiel lautet 0,367879441.

Klicken Sie auf OK, um die Antwort in die ausgewählte Zelle einzufügen.

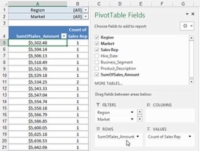
Im Beispiel sehen Sie die Wahrscheinlichkeit für zwei defekte Gelenke von 1.000 und die Wahrscheinlichkeit für drei. Um die Berechnungen durchzuführen, geben Sie 2 in das Feld X ein, um pr (2) zu berechnen , und 3 , um pr (3) zu finden .

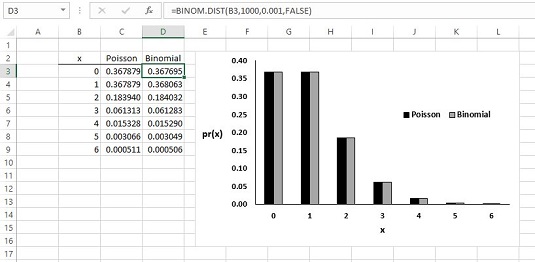
Im 21. Jahrhundert ist es ziemlich einfach, die Binomialwahrscheinlichkeiten direkt zu berechnen. Das Bild unten zeigt Ihnen die Poisson- und die Binomial-Wahrscheinlichkeiten für die Zahlen in Spalte B und die Bedingungen des Beispiels. Die Wahrscheinlichkeiten werden grafisch dargestellt, damit Sie sehen können, wie nahe die beiden wirklich sind. Zelle D3 wurde ausgewählt, daher zeigt Ihnen die Formelleiste, wie BINOM.VERT verwendet wurde, um die Binomialwahrscheinlichkeiten zu berechnen.

Obwohl die Nützlichkeit des Poisson als Näherung veraltet ist, hat er ein Eigenleben entwickelt. Phänomene, die so unterschiedlich sind wie die Reaktionszeitdaten in psychologischen Experimenten, die Degeneration radioaktiver Substanzen und die Ergebnisse bei professionellen Hockeyspielen, scheinen in die Poisson-Verteilungen zu passen. Aus diesem Grund stützen sich Wirtschaftsanalysten und wissenschaftliche Forscher gerne auf Modelle auf dieser Verteilung.