Verwenden der hypergeometrischen Verteilung für die statistische Analyse mit Excel

Die hypergeometrische Verteilung befasst sich mit Erfolgen und Misserfolgen und ist nützlich für die statistische Analyse mit Excel. Beginnen wir mit einem Beispiel. In einem Satz von 16 Glühbirnen sind 9 gut und 7 defekt. Wenn Sie zufällig 6 Glühbirnen aus diesen 16 auswählen, wie groß ist die Wahrscheinlichkeit, dass 3 der 6 gut sind? Ziehen Sie die Wahl einer guten Glühbirne als „Erfolg“ in Betracht.

Wenn Sie mit der Auswahl fertig sind, besteht Ihre Auswahl aus einer Kombination von drei der neun guten Glühbirnen zusammen mit einer Kombination von drei der sieben defekten Glühbirnen. Die Wahrscheinlichkeit, drei gute Glühbirnen zu bekommen, ist a. . . Gut . . . Kombination von Zählregeln.

Jedes Ergebnis der Auswahl der guten Glühbirnen kann mit allen Ergebnissen der Auswahl der defekten Glühbirnen verknüpft werden, so dass die Produktregel für den Zähler angemessen ist. Der Nenner (der Stichprobenraum) ist die Anzahl der möglichen Kombinationen von 6 Items in einer Gruppe von 16 Items.

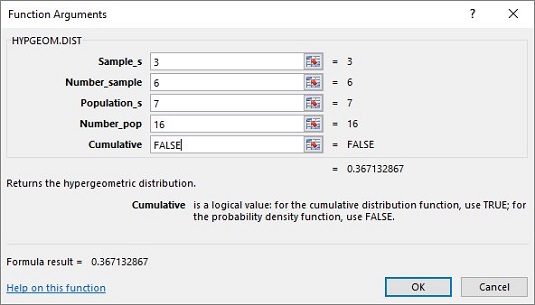
HYPGEOM.DIST berechnet alles für Sie, wenn es um die hypergeometrische Verteilung geht. So verwenden Sie es, um das vorherige Beispiel durchzuarbeiten:

Wählen Sie eine Zelle für die Antwort von HYPGEOM.DIST aus.

Wählen Sie im Menü Statistische Funktionen die Option HYPGEOM.VERT aus, um das Dialogfeld Funktionsargumente zu öffnen.

Geben Sie im Dialogfeld Funktionsargumente die entsprechenden Werte für die Argumente ein.
Geben Sie im Feld Sample_s die Anzahl der Erfolge in der Probe ein. Diese Zahl ist für dieses Beispiel 3.
Geben Sie im Feld Number_sample die Anzahl der Elemente in der Stichprobe ein. Die Stichprobengröße für dieses Beispiel beträgt 6.
Geben Sie im Feld Population_s die Anzahl der Erfolge in der Population ein. In diesem Beispiel sind das 7 gute Glühbirnen.
Geben Sie im Feld Number_pop die Anzahl der Elemente in der Population ein. Die Gesamtzahl der Glühbirnen beträgt 16, und das ist die Bevölkerungszahl.
Geben Sie im Feld Kumulativ FALSE ein. Dies gibt die Wahrscheinlichkeit der Anzahl von Erfolgen an, die Sie in das Feld Sample_s eingegeben haben. Wenn Sie TRUE eingeben, gibt die Funktion die Wahrscheinlichkeit von maximal dieser Anzahl von Erfolgen zurück (z. B. die kumulierte Wahrscheinlichkeit).
Wenn für alle Argumente Werte eingegeben wurden, wird die Antwort im Dialogfeld angezeigt. Die Antwort lautet 0,367 und einige zusätzliche Dezimalstellen.Klicken Sie auf OK, um die Antwort in die ausgewählte Zelle einzufügen.

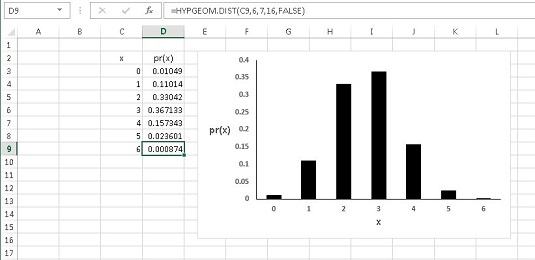
Sie können HYP.GEOM.DIST verwenden, um pr (0) bis pr (6) für dieses Beispiel zu berechnen . Anschließend verwenden Sie die Grafikfunktionen von Excel, um die Ergebnisse grafisch darzustellen. Das Ziel besteht darin, Ihnen zu helfen, die hypergeometrische Verteilung zu visualisieren und zu verstehen.