如何規範化 NumPy 數組：快速指南

如果您一直在使用 Python 進行數據分析或機器學習，那麼您可能遇到過 NumPy 數組。它們是處理數值數據的強大工具，但有時需要調整或“規範化”這些數組中的數據，以便在您的算法中有效使用。但是規範化一個數組是什麼意思呢？

要規範化 NumPy 數組，您必須調整數組中的值，使它們落在特定範圍內，通常在 0 和 1 之間，或者使它們具有標準正態分佈，均值為 0，標準差為 1機器學習和數據分析領域經常這樣做，以確保所有輸入特徵具有相同的尺度。

在本文中，我們將探討如何在 Python 中規範化 NumPy 數組。我們將了解可用於規範化 NumPy 數組的不同方法，並查看示例以幫助您更好地理解該概念。

讓我們開始吧！

目錄

• Python 規範化的基礎是什麼？
  • 什麼是歸一化？
  • 為什麼規範化很重要？
  • 什麼是規範？
  • 什麼是機器學習中的規範化？
• Python 中的規範化技術有哪些？
  • 1. 如何進行最小-最大縮放
  • 2. 如何進行 L1 歸一化
  • 3. 如何進行 L2 歸一化
• 如何在 Python 中使用 Scikit-Learn 進行規範化
  • 1. 如何使用 MinMaxScaler 規範化數組
  • 2.如何執行就地行規範化
• 最後的想法

Python 規範化的基礎是什麼？

在我們用 Python 實現規範化之前，您必須了解規範化的含義。

因此，在本節中，我們將討論什麼是規範化及其核心概念。

什麼是歸一化？

規範化是將數據縮放和轉換為標準化範圍的過程。這是通過將數據的每個元素除以一個參數來完成的。該參數可以是最大值、範圍或其他一些範數。

您可以使用歐幾里德範數（也稱為 L2 範數）對 NumPy 數組進行歸一化。此外，您還可以通過在特定範圍（通常為 0 到 1）之間重新縮放值來規範化 NumPy 數組。

在 Python 中，NumPy 庫提供了一種高效的數組規範化方法。這也包括多維數組和矩陣。

為什麼規範化很重要？

歸一化很重要，因為它可以確保在比較和分析數據時平等對待不同的特徵。您可以使用它來消除由於不同比例而可能出現的潛在偏差或差異。

什麼是規範？

用於歸一化的參數可以是不同的範數，例如歐幾里得範數 (L2)、曼哈頓範數 (L1) 或最大範數 (L_inf)。您使用範數來計算向量或矩陣的大小。然後將這些用作比例因子以規範化數據。

在處理矩陣時，我們經常使用Frobenius 範數，它是多維數組的歐幾里得範數的推廣。

以下示例顯示了使用 Frobenius 範數對矩陣進行歸一化：

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
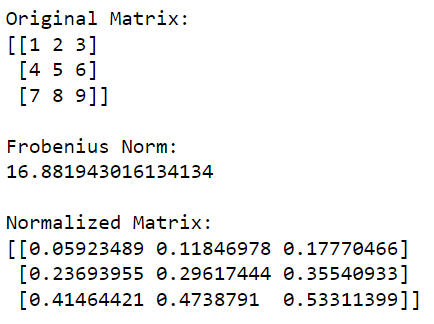
print(normalized_matrix)

此 Python 代碼將首先導入 NumPy 庫並使用它來創建矩陣。然後計算矩陣的 Frobenius 範數，然後將矩陣中的每個元素除以該值以對其進行歸一化。

此代碼的輸出如下所示：

什麼是機器學習中的規範化？

在機器學習中，歸一化是一個重要的預處理步驟，因為它可以提高算法的性能。

在執行基於梯度的優化技術時，您會發現優化後的特徵往往會更快更有效地收斂。這是因為它降低了縮放不良或梯度消失的風險。

Python 中的規範化技術有哪些？

您可以通過多種方式執行NumPy數組的規範化。但是，由於效率高，某些方法比其他方法更受歡迎。

在本節中，我們將了解三種廣泛使用的歸一化技術：

1. 最小-最大縮放

2. L1歸一化

3. L2 歸一化

1. 如何進行最小-最大縮放

最小-最大縮放也稱為線性歸一化或特徵縮放。在最小-最大縮放中，我們縮放 NumPy 數組的值，使它們落在指定範圍內，通常在 0 和 1 之間。

為此，您從每個元素中減去最小值，並將結果除以最大值和最小值之間的差值。

您可以在數學上將最小-最大縮放比例表示為：

x' = (x - min(x)) / (max(x) - min(x))

以下示例演示瞭如何使用 NumPy 庫執行最小-最大縮放：

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

此代碼將首先導入 NumPy，然後計算矩陣中的最小值和最大值，然後對其進行縮放，使所有值都在 0（對應於原始最小值）和 1（對應於原始最大值）之間。

此代碼的輸出如下所示：

最小-最大縮放是機器學習和數據預處理中非常常見的縮放形式。

2. 如何進行 L1 歸一化

L1 歸一化使用 L1 範數，它是數組元素的絕對值之和。這對於稀疏矩陣特別有用。它確保歸一化數組元素的絕對值之和等於 1。

L1歸一化的公式為：

x' = x / sum(|x|)

以下示例顯示瞭如何使用 NumPy 執行 L1 規範化：

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
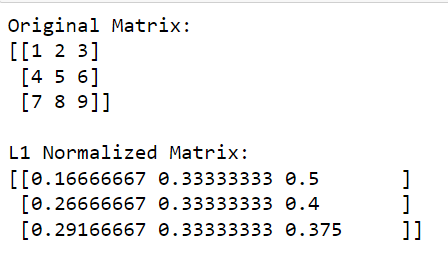
print(l1_normalized_matrix)

在此代碼中，np.linalg.norm (matrix, 1, axis=1, keepdims=True) 計算每一行的 L1 範數（這是通過指定 axis=1 完成的）。

此操作將返回一個列向量，其中每個元素都是相應行的 L1 範數。通過將原始矩陣除以這些範數（按元素執行除法），我們獲得了矩陣的 L1 歸一化版本。

輸出如下：

3. 如何進行 L2 歸一化

L2 歸一化使用 L2 範數，它是數組元素平方和的平方根。

該方法將歸一化數組轉換為 2-範數為 1 的單位向量。L2 歸一化對於降維很有用，並確保所有特徵同等重要。

L2歸一化的公式為：

x' = x / sqrt(sum(x^2))

這是使用NumPy執行 L2 規範化的方法：

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
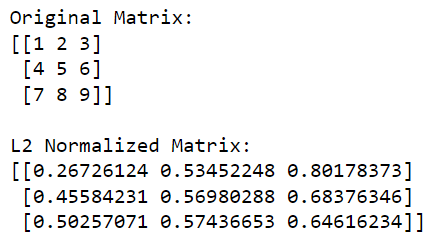
print(l2_normalized_matrix)

在此代碼中，np.linalg.norm(matrix, 2, axis=1, keepdims=True)計算每一行的 L2 範數（歐幾里德範數）（這是通過指定 axis=1 來完成的）。此操作將返回一個列向量，其中每個元素都是相應行的 L2 範數。

通過將原始矩陣除以這些範數（按元素執行除法），我們獲得了矩陣的 L2 歸一化版本。

輸出如下：

好了，現在我們已經了解了使用 NumPy 創建規範化數組的流行方法，讓我們在下一節中看看如何使用其他 Python 庫執行相同的操作。

如何在 Python 中使用 Scikit-Learn 進行規範化

Scikit-learn 是一個強大的機器學習 Python 庫。它提供了多種數據預處理工具。

您可以使用的一個工具是sklearn.preprocessing模塊，它提供了多種技術來執行規範化。有許多不同的定標器函數、轉換器和歸一化器可用。但是，我們將專注於MinMaxScaler和normalize 函數。

要使用 scikit-learn 預處理數據，您主要使用 transformer API。這包括fit、transform和fit_transform方法。

1. 如何使用 MinMaxScaler 規範化數組

MinMaxScaler是一種將數據歸一化到指定範圍（通常為 [0, 1]）的縮放器。

MinMaxScalar 的公式如下：

scaled_value = (value - min_value) / (max_value - min_value)

要實現MinMaxScaler，您可以按照以下步驟操作：

1. 導入所需的庫：

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. 創建一個 NumPy 數組：

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. 實例化MinMaxScaler並將其擬合到數據中：

   scaler = MinMaxScaler()
   scaler.fit(data)

4. 使用transform或fit_transform方法轉換數據：

   normalized_data = scaler.transform(data)

此代碼的輸出如下所示：

正如您在輸出中看到的那樣，MinMaxScalarMatrix 的值範圍僅為 0 到 1。

2.如何執行就地行規範化

您還可以使用就地行規範化作為替代方法，使用normalize函數。

此方法通過將向量縮放為單位範數來獨立地對每個輸入數組或特徵進行歸一化。默認情況下，normalize函數使用 L2 範數執行簡單歸一化，但您可以選擇其他範數選項。

以下示例演示了就地行規範化：

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
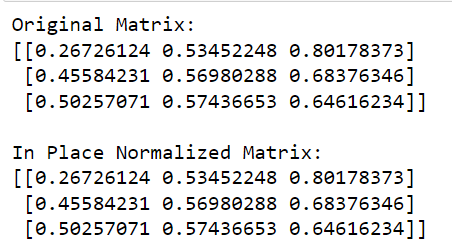
print(matrix)

在此代碼中，我們從sklearn調用規範化函數，定義要使用的規範（在本例中為“l2”），並設置copy=False以執行就地規範化。

此代碼的輸出如下所示：

要了解有關Python機器學習的更多信息，請查看以下視頻：

最後的想法

隨著您進一步探索數據科學和機器學習，您會發現規範化過程是數據預處理管道中必不可少的一步。

首先，它將不同的特徵放在一個共同的尺度上。這使您的模型對輸入規模不太敏感。它可以極大地提高許多機器學習算法的性能。

其次，它可以幫助您加快培訓過程。一些算法，尤其是那些基於計算距離計算的算法，在數據標準化時收斂得更快。

通過學習如何規範化數據，您可以掌握一項關鍵技能。歸一化是在實際應用中經常使用的實用工具。它將幫助您減少由於異常值或單位差異而導致意外結果的可能性。

與任何工具一樣，掌握規範化的關鍵在於實踐。因此，請不要猶豫，動手嘗試不同的數據集和隨機值。數據科學的世界是你的牡蠣。編碼愉快！