Come normalizzare gli array NumPy: una guida rapida

Se hai lavorato con Python per l'analisi dei dati o l'apprendimento automatico, probabilmente ti sei imbattuto in array NumPy. Sono un potente strumento per la gestione dei dati numerici, ma a volte i dati all'interno di questi array devono essere regolati o "normalizzati" per essere utilizzati efficacemente nei tuoi algoritmi. Ma cosa significa normalizzare un array?

Per normalizzare un array NumPy, devi regolare i valori nell'array in modo che rientrino in un certo intervallo, in genere tra 0 e 1, o in modo che abbiano una distribuzione normale standard con una media di 0 e una deviazione standard di 1 Questo viene spesso fatto nel campo dell'apprendimento automatico e dell'analisi dei dati per garantire che tutte le funzionalità di input abbiano la stessa scala.

In questo articolo, esploreremo come normalizzare un array NumPy in Python. Esamineremo i diversi metodi che puoi utilizzare per normalizzare un array NumPy e esamineremo anche esempi per aiutarti a comprendere meglio il concetto.

Entriamo in esso!

Sommario

• Quali sono le basi della normalizzazione in Python?
  • Cos'è la normalizzazione?
  • Perché è importante la normalizzazione?
  • Cosa sono le norme?
  • Che cos'è la normalizzazione nell'apprendimento automatico?
• Quali sono le tecniche di normalizzazione in Python?
  • 1. Come eseguire il ridimensionamento min-max
  • 2. Come eseguire la normalizzazione L1
  • 3. Come eseguire la normalizzazione L2
• Come utilizzare Scikit-Learn per la normalizzazione in Python
  • 1. Come normalizzare l'array utilizzando MinMaxScaler
  • 2. Come eseguire la normalizzazione delle righe sul posto
• Pensieri finali

Quali sono le basi della normalizzazione in Python?

Prima di implementare la normalizzazione in Python, devi capire cosa significa normalizzazione.

Pertanto, in questa sezione, esamineremo cos'è la normalizzazione e i suoi concetti fondamentali.

Cos'è la normalizzazione?

La normalizzazione è un processo che ridimensiona e trasforma i dati in un intervallo standardizzato. Questo viene fatto dividendo ogni elemento dei dati per un parametro. Il parametro può essere il valore massimo, l'intervallo o qualche altra norma.

È possibile normalizzare l'array NumPy utilizzando la norma euclidea (nota anche come norma L2). Inoltre, puoi anche normalizzare gli array NumPy ridimensionando i valori tra un certo intervallo, in genere da 0 a 1.

In Python, la libreria NumPy fornisce un modo efficiente per normalizzare gli array. Ciò include anche array e matrici multidimensionali.

Perché è importante la normalizzazione?

La normalizzazione è importante in quanto garantisce che caratteristiche diverse vengano trattate allo stesso modo durante il confronto e l'analisi dei dati. Puoi usarlo per eliminare potenziali pregiudizi o discrepanze che potrebbero sorgere a causa di scale diverse.

Cosa sono le norme?

Il parametro utilizzato per la normalizzazione può essere norme diverse , ad esempio la norma euclidea (L2), la norma Manhattan (L1) o la norma massima (L_inf). Si usano le norme per calcolare la grandezza di un vettore o di una matrice . Questi vengono quindi utilizzati come fattore di scala per normalizzare i dati.

Quando lavoriamo con le matrici, usiamo spesso la norma di Frobenius , che è una generalizzazione della norma euclidea per gli array multidimensionali.

L'esempio seguente mostra la normalizzazione di una matrice utilizzando la norma di Frobenius:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
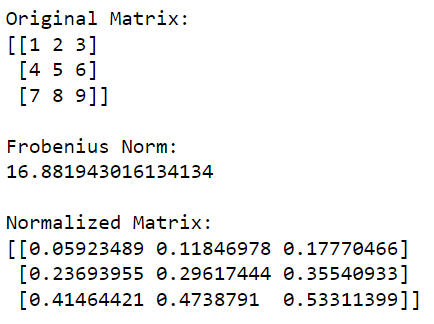
print(normalized_matrix)

Questo codice Python importerà prima la libreria NumPy e la utilizzerà per creare una matrice. Quindi calcola la norma di Frobenius della matrice e quindi divide ogni elemento nella matrice per questo valore per normalizzarlo.

L'output di questo codice è riportato di seguito:

Che cos'è la normalizzazione nell'apprendimento automatico?

Nell'apprendimento automatico , la normalizzazione è un importante passaggio di pre-elaborazione in quanto migliora le prestazioni degli algoritmi.

Quando esegui tecniche di ottimizzazione basate sul gradiente, scoprirai che le funzionalità ottimizzate tendono a convergere in modo più rapido ed efficiente. Questo perché riduce il rischio di scarso ridimensionamento o gradienti che svaniscono.

Quali sono le tecniche di normalizzazione in Python?

È possibile eseguire la normalizzazione degli array NumPy in diversi modi. Tuttavia, alcuni metodi sono più popolari di altri a causa della loro elevata efficienza.

Per questa sezione, esamineremo le tre tecniche di normalizzazione ampiamente utilizzate:

1. Ridimensionamento minimo-massimo

2. Normalizzazione L1

3. Normalizzazione L2

1. Come eseguire il ridimensionamento min-max

Il ridimensionamento min-max è anche noto come normalizzazione lineare o ridimensionamento delle caratteristiche. Nel ridimensionamento min-max, ridimensioniamo i valori di un array NumPy in modo che rientrino in un intervallo specificato, in genere tra 0 e 1.

Per fare ciò, sottrai il valore minimo da ciascun elemento e dividi il risultato per la differenza tra i valori massimo e minimo.

Puoi rappresentare matematicamente il ridimensionamento min-max come:

x' = (x - min(x)) / (max(x) - min(x))

L'esempio seguente mostra come eseguire il ridimensionamento min-max utilizzando la libreria NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Questo codice importerà prima NumPy e quindi calcolerà i valori minimo e massimo nella matrice, che quindi ridimensionerà in modo tale che tutti i valori siano compresi tra 0 (corrispondente al valore minimo originale) e 1 (corrispondente al valore massimo originale).

L'output di questo codice è riportato di seguito:

Il ridimensionamento min-max è una forma molto comune di ridimensionamento nell'apprendimento automatico e nella preelaborazione dei dati.

2. Come eseguire la normalizzazione L1

La normalizzazione L1 utilizza la norma L1, che è la somma dei valori assoluti degli elementi dell'array. Ciò è particolarmente utile per le matrici sparse. Assicura che la somma dei valori assoluti degli elementi dell'array normalizzati sia uguale a 1.

La formula per la normalizzazione L1 è:

x' = x / sum(|x|)

L'esempio seguente mostra come eseguire la normalizzazione L1 utilizzando NumPy:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
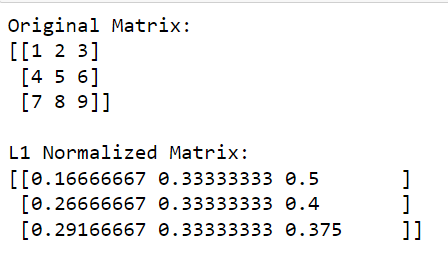
print('nL1 Normalized Matrix:')
print(l1_normalized_matrix)

In questo codice, np.linalg.norm (matrix, 1, axis=1, keepdims=True) calcola la norma L1 per ogni riga (questo viene fatto specificando axis=1).

Questa operazione restituirà un vettore colonna in cui ogni elemento è la norma L1 della riga corrispondente. Dividendo la matrice originale per queste norme (eseguendo la divisione per elemento), otteniamo la versione L1 normalizzata della matrice.

L'output è riportato di seguito:

3. Come eseguire la normalizzazione L2

La normalizzazione L2 utilizza la norma L2, che è la radice quadrata della somma degli elementi quadrati dell'array.

Questo metodo converte l'array normalizzato in un vettore unitario con una norma 2 pari a 1. La normalizzazione L2 è utile per la riduzione dimensionale e garantisce uguale importanza per tutte le caratteristiche.

La formula per la normalizzazione L2 è:

x' = x / sqrt(sum(x^2))

Ecco come eseguire la normalizzazione L2 usando NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
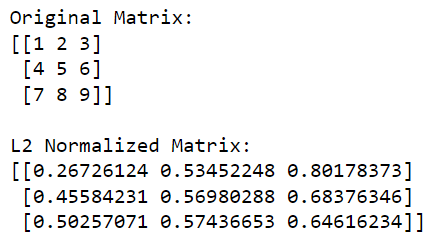
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

In questo codice, np.linalg.norm(matrix, 2, axis=1, keepdims=True) calcola la norma L2 (norma euclidea) per ogni riga (ciò viene fatto specificando axis=1). Questa operazione restituirà un vettore colonna in cui ogni elemento è la norma L2 della riga corrispondente.

Dividendo la matrice originale per queste norme (eseguendo la divisione per elemento), otteniamo la versione L2 normalizzata della matrice.

L'output è riportato di seguito:

Bene, ora che abbiamo esaminato i modi più diffusi per creare un array normalizzato utilizzando NumPy, diamo un'occhiata a come puoi fare lo stesso utilizzando altre librerie Python nella sezione successiva.

Come utilizzare Scikit-Learn per la normalizzazione in Python

Scikit-learn è una potente libreria Python per l'apprendimento automatico. Fornisce diversi strumenti per la preelaborazione dei dati.

Uno strumento che puoi utilizzare è il modulo sklearn.preprocessing , che offre varie tecniche per eseguire la normalizzazione. Sono disponibili molte diverse funzioni scaler, trasformatori e normalizzatori. Tuttavia, ci concentreremo su MinMaxScaler e sulla funzione normalize .

Per preelaborare i dati con scikit-learn, si utilizza principalmente l'API del trasformatore. Ciò include i metodi fit , transform e fit_transform .

1. Come normalizzare l'array utilizzando MinMaxScaler

MinMaxScaler è uno scaler che normalizza i dati in un intervallo specificato, in genere [0, 1] .

La formula per MinMaxScalar è riportata di seguito:

scaled_value = (value - min_value) / (max_value - min_value)

Per implementare MinMaxScaler , puoi seguire questi passaggi:

1. Importa le librerie richieste:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Crea un array NumPy:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Crea un'istanza di MinMaxScaler e adattala ai dati:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Trasforma i dati utilizzando il metodo transform o fit_transform :

   normalized_data = scaler.transform(data)

L'output di questo codice è riportato di seguito:

Come puoi vedere nell'output che MinMaxScalarMatrix ha solo valori compresi tra 0 e 1.

2. Come eseguire la normalizzazione delle righe sul posto

In alternativa, puoi anche utilizzare la normalizzazione delle righe sul posto, utilizzando la funzione normalize .

Questo metodo normalizza ogni matrice o caratteristica di input in modo indipendente ridimensionando il vettore a una norma unitaria. Per impostazione predefinita, la funzione di normalizzazione utilizza la norma L2 per eseguire la normalizzazione semplice, ma è possibile scegliere altre opzioni di norma.

L'esempio seguente mostra la normalizzazione delle righe sul posto:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

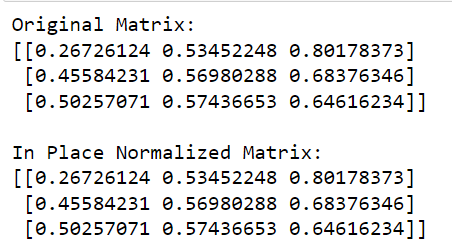
print('L2 Normalized Matrix:')
print(matrix)

In questo codice chiamiamo la funzione normalize da sklearn , definiamo la norma da usare ('l2' in questo caso) e impostiamo copy=False per eseguire la normalizzazione sul posto.

L'output di questo codice è riportato di seguito:

Per ulteriori informazioni sull'apprendimento automatico in Python , guarda il seguente video:

Pensieri finali

Mentre esplori ulteriormente la scienza dei dati e l'apprendimento automatico, scoprirai che il processo di normalizzazione è un passaggio essenziale nella tua pipeline di preelaborazione dei dati.

In primo luogo, pone diverse caratteristiche su una scala comune. Ciò rende i tuoi modelli meno sensibili alla scala degli input. Può migliorare notevolmente le prestazioni di molti algoritmi di apprendimento automatico.

In secondo luogo, ti aiuta ad accelerare il processo di formazione. Alcuni algoritmi, in particolare quelli basati su calcoli di distanza calcolati, convergono più velocemente quando i dati vengono normalizzati.

Imparando a normalizzare i dati, ti doti di un'abilità cruciale. La normalizzazione è uno strumento pratico utilizzato abitualmente nelle applicazioni del mondo reale. Ti aiuterà a ridurre la probabilità di risultati imprevisti dovuti a valori anomali o differenze nelle unità.

Come ogni strumento, la chiave per padroneggiare la normalizzazione sta nella pratica. Quindi, non esitare a sporcarti le mani e sperimentare diversi set di dati e valori casuali. Il mondo della scienza dei dati è la tua ostrica. Buona programmazione!