NumPy 配列を正規化する方法: クイックガイド

データ分析や機械学習のために Python を使用している場合は、NumPy 配列に遭遇したことがあるでしょう。これらは数値データを処理するための強力なツールですが、場合によっては、アルゴリズムで効果的に使用するために、これらの配列内のデータを調整または「正規化」する必要があります。しかし、配列を正規化するとはどういう意味でしょうか?

NumPy 配列を正規化するには、配列内の値を特定の範囲 (通常は 0 ～ 1) 内に収まるように、または平均 0、標準偏差 1 の標準正規分布になるように調整する必要があります。これは、すべての入力特徴が同じスケールであることを保証するために、機械学習やデータ分析の分野でよく行われます。

この記事では、Python で NumPy 配列を正規化する方法を検討します。NumPy 配列を正規化するために使用できるさまざまな方法を見て、概念をよりよく理解するのに役立つ例も見ていきます。

さあ、始めましょう！

目次

• Python における正規化の基本とは何ですか?
  • 正規化とは何ですか?
  • 正規化が重要なのはなぜですか?
  • 規範とは何ですか?
  • 機械学習における正規化とは何ですか?
• Python の正規化テクニックとは何ですか?
  • 1. 最小-最大スケーリングを実行する方法
  • 2. L1 正規化の実行方法
  • 3. L2 正規化の実行方法
• Python での正規化に Scikit-Learn を使用する方法
  • 1. MinMaxScaler を使用して配列を正規化する方法
  • 2. インプレース行正規化を実行する方法
• 最終的な考え

Python における正規化の基本とは何ですか?

Python で正規化を実装する前に、正規化の意味を理解する必要があります。

したがって、このセクションでは、正規化とは何か、およびその中心となる概念について説明します。

正規化とは何ですか?

正規化は、データをスケーリングして標準化された範囲に変換するプロセスです。これは、データの各要素をパラメータで分割することによって行われます。パラメータには、最大値、範囲、またはその他の基準を指定できます。

ユークリッド ノルム (L2 ノルムとも呼ばれます) を使用して NumPy 配列を正規化できます。さらに、特定の範囲 (通常は 0 から 1) の間で値を再スケーリングすることで、NumPy 配列を正規化することもできます。

Python では、NumPy ライブラリは配列を正規化する効率的な方法を提供します。これには、多次元配列や行列も含まれます。

正規化が重要なのはなぜですか?

正規化は、データを比較および分析するときにさまざまな特徴が同等に扱われることを保証するため重要です。これを使用すると、スケールの違いによって生じる可能性のある潜在的なバイアスや不一致を排除できます。

規範とは何ですか?

正規化に使用するパラメータには、ユークリッド ノルム (L2)、マンハッタン ノルム (L1)、最大ノルム (L_inf) などのさまざまなノルムを使用できます。ノルムを使用して、ベクトルまたは行列の大きさを計算します。これらは、データを正規化するための倍率として使用されます。

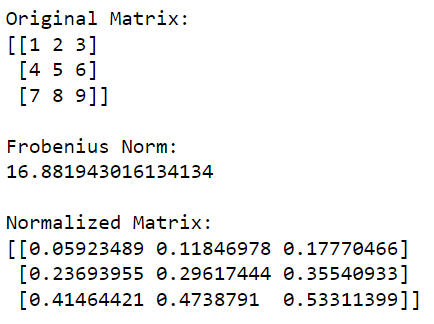
行列を扱うときは、多次元配列のユークリッド ノルムを一般化したフロベニウス ノルムをよく使用します。

次の例は、フロベニウス ノルムを使用した行列の正規化を示しています。

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
print(normalized_matrix)

この Python コードは、まず NumPy ライブラリをインポートし、それを使用して行列を作成します。次に、行列のフロベニウス ノルムを計算し、行列内の各要素をこの値で除算して正規化します。

このコードの出力は次のとおりです。

機械学習における正規化とは何ですか?

機械学習では、正規化はアルゴリズムのパフォーマンスを向上させるため、重要な前処理ステップです。

勾配ベースの最適化手法を実行すると、最適化された特徴がより迅速かつ効率的に収束する傾向があることがわかります。これは、スケーリングが不十分になったり、グラデーションが消えたりするリスクが軽減されるためです。

Python の正規化テクニックとは何ですか?

NumPy配列の正規化はさまざまな方法で実行できます。ただし、効率が高いため、他の方法よりも人気のある方法もあります。

このセクションでは、広く使用されている 3 つの正規化手法を見ていきます。

1. 最小-最大スケーリング

2. L1 正規化

3. L2 正規化

1. 最小-最大スケーリングを実行する方法

最小-最大スケーリングは、線形正規化または特徴スケーリングとも呼ばれます。min-max スケーリングでは、NumPy 配列の値を、指定された範囲 (通常は 0 から 1) 内に収まるようにスケーリングします。

これを行うには、各要素から最小値を減算し、その結果を最大値と最小値の差で割ります。

最小-最大スケーリングは数学的に次のように表すことができます。

x' = (x - min(x)) / (max(x) - min(x))

次の例は、NumPy ライブラリを使用して最小-最大スケーリングを実行する方法を示しています。

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

このコードは、最初に NumPy をインポートし、次に行列の最小値と最大値を計算します。次に、すべての値が 0 (元の最小値に対応) と 1 (元の最大値に対応) の間に収まるようにスケーリングします。

このコードの出力は次のとおりです。

Min-Max スケーリングは、機械学習とデータの前処理における非常に一般的な形式のスケーリングです。

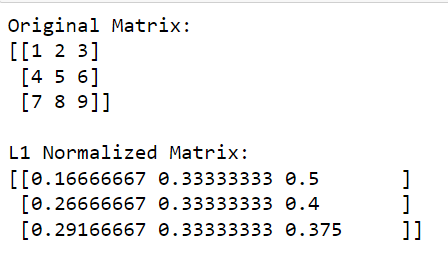
2. L1 正規化の実行方法

L1 正規化では、配列要素の絶対値の合計である L1 ノルムが使用されます。これは、スパース行列に特に役立ちます。これにより、正規化された配列要素の絶対値の合計が 1 に等しくなることが保証されます。

L1 正規化の式は次のとおりです。

x' = x / sum(|x|)

次の例は、NumPy を使用して L1 正規化を実行する方法を示しています。

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
print(l1_normalized_matrix)

このコードでは、np.linalg.norm (matrix, 1, axis=1, keepdims=True) は各行の L1 ノルムを計算します (これは axis=1 を指定することで実行されます)。

この演算は、各要素が対応する行の L1 ノルムである列ベクトルを返します。元の行列をこれらのノルムで除算する (要素ごとに除算を実行する) ことにより、行列の L1 正規化バージョンが得られます。

出力は以下のとおりです。

3. L2 正規化の実行方法

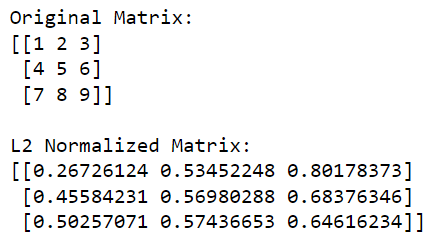
L2 正規化では、配列要素の二乗の合計の平方根である L2 ノルムが使用されます。

このメソッドは、正規化された配列を 2 ノルム 1 の単位ベクトルに変換します。L2 正規化は次元削減に役立ち、すべての特徴の重要性が同等であることが保証されます。

L2 正規化の式は次のとおりです。

x' = x / sqrt(sum(x^2))

NumPyを使用して L2 正規化を実行する方法は次のとおりです。

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

このコードでは、np.linalg.norm(matrix, 2, axis=1, keepdims=True) は各行の L2 ノルム (ユークリッド ノルム) を計算します (これは axis=1 を指定することで実行されます)。この演算は、各要素が対応する行の L2 ノルムである列ベクトルを返します。

元の行列をこれらのノルムで除算する (要素ごとに除算を実行する) ことにより、行列の L2 正規化バージョンが得られます。

出力は以下のとおりです。

さて、NumPy を使用して正規化配列を作成する一般的な方法を説明したので、次のセクションで他の Python ライブラリを使用して同じことを行う方法を見てみましょう。

Python での正規化に Scikit-Learn を使用する方法

Scikit-learn は、機械学習用の強力な Python ライブラリです。データの前処理のためのいくつかのツールが提供されます。

使用できるツールの 1 つはsklearn.preprocessingモジュールで、これは正規化を実行するためのさまざまな手法を提供します。さまざまなスケーラー関数、トランスフォーマー、ノーマライザーが利用可能です。ただし、 MinMaxScalerと正規化 関数に焦点を当てます。

scikit-learn でデータを前処理するには、主にトランスフォーマー API を使用します。これには、fit、transform、およびfit_transformメソッドが含まれます。

1. MinMaxScaler を使用して配列を正規化する方法

MinMaxScaler は、データを指定された範囲 (通常は [0, 1]) に正規化するスケーラーです。

MinMaxScalar の式は次のとおりです。

scaled_value = (value - min_value) / (max_value - min_value)

MinMaxScalerを実装するには、次の手順に従います。

1. 必要なライブラリをインポートします。

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. NumPy 配列を作成します。

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. MinMaxScalerをインスタンス化してデータに適合させます。

   scaler = MinMaxScaler()
   scaler.fit(data)

4. transformまたはfit_transformメソッドを使用してデータを変換します。

   normalized_data = scaler.transform(data)

このコードの出力は次のとおりです。

出力からわかるように、MinMaxScalarMatrixには 0 ～ 1 の範囲の値のみが含まれます。

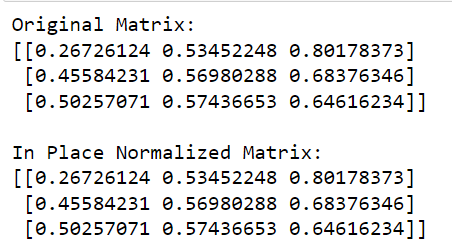
2. インプレース行正規化を実行する方法

代わりに、 normalize関数を使用して、インプレース行正規化を使用することもできます。

このメソッドは、ベクトルを単位ノルムにスケーリングすることによって、各入力配列または特徴を個別に正規化します。デフォルトでは、正規化関数は L2 ノルムを使用して単純な正規化を実行しますが、他のノルム オプションを選択することもできます。

次の例は、インプレース行正規化を示しています。

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
print(matrix)

このコードでは、 sklearnから正規化関数を呼び出し、使用するノルム (この場合は「l2」) を定義し、インプレース正規化を実行するためにcopy=Falseを設定します。

このコードの出力は次のとおりです。

Pythonでの機械学習の詳細については、次のビデオをご覧ください。

最終的な考え

データ サイエンスと機械学習をさらに詳しく調査すると、正規化プロセスがデータ前処理パイプラインの重要なステップであることがわかります。

まず、さまざまな機能を共通のスケールに配置します。これにより、モデルは入力のスケールにあまり影響されなくなります。これにより、多くの機械学習アルゴリズムのパフォーマンスが大幅に向上します。

次に、トレーニング プロセスのスピードアップに役立ちます。一部のアルゴリズム、特に計算された距離の計算に基づくアルゴリズムは、データが正規化されるとより速く収束します。

データを正規化する方法を学ぶことで、重要なスキルを身につけることができます。正規化は、現実のアプリケーションで日常的に使用される実用的なツールです。これは、外れ値や単位の違いによって予期しない結果が発生する可能性を減らすのに役立ちます。

他のツールと同様に、正規化を習得するための鍵は実践にあります。したがって、ためらわずに実際に手を動かし、さまざまなデータセットやランダム値を試してみてください。データ サイエンスの世界はあなたの好みに合わせて選べます。コーディングを楽しんでください!