Phân phối f là phân phối xác suất trong Excel so sánh tỷ lệ theo phương sai của các mẫu được lấy từ các quần thể khác nhau. Sự so sánh đó tạo ra một kết luận về việc liệu các phương sai trong các quần thể cơ bản có giống nhau hay không.
Hàm F.DIST trả về xác suất bên trái của việc quan sát tỷ lệ phương sai của hai mẫu lớn bằng một giá trị f được chỉ định. Hàm sử dụng cú pháp
= F.DIST (x, deg_freedom1, deg_freedom2, tích lũy)
trong đó x được chỉ định giá trị f mà bạn muốn kiểm tra; deg_freedom1 là bậc tự do trong mẫu đầu tiên hoặc tử số; deg_freedom2 là bậc tự do trong mẫu thứ hai, hoặc mẫu số, và tích lũy là một giá trị logic (0 hoặc 1) cho Excel biết bạn muốn tính toán phân phối tích lũy (được biểu thị bằng cách đặt tích lũy thành 0) hay mật độ xác suất ( được chỉ ra bằng cách đặt tích lũy thành 1).
Để làm ví dụ về cách hoạt động của hàm F.DIST, giả sử bạn so sánh hai phương sai của mẫu, một bằng và một bằng. Điều này có nghĩa là giá trị f bằng. Ngoài ra, giả sử rằng cả hai mẫu đều đánh số 10 mục, có nghĩa là cả hai mẫu đều có bậc tự do bằng nhau và bạn muốn tính xác suất tích lũy. Công thức
= F.DIST (2 / 4,9,9,0)
trả về giá trị 0,6851816.
Hàm F.DIST.RT tương tự như hàm F.DIST. F.DIST.RT trả về xác suất bên phải của việc quan sát tỷ lệ phương sai của hai mẫu lớn bằng một giá trị f được chỉ định. Hàm sử dụng cú pháp
= F.DIST.RT (x, deg_freedom1, deg_freedom2, tích lũy)
trong đó x được chỉ định giá trị f mà bạn muốn kiểm tra; deg_freedom1 là bậc tự do trong mẫu đầu tiên hoặc tử số; deg_freedom2 là bậc tự do trong mẫu thứ hai, hoặc mẫu số, và tích lũy là một giá trị logic (0 hoặc 1) cho Excel biết bạn muốn tính toán phân phối tích lũy (được biểu thị bằng cách đặt tích lũy thành 0) hay mật độ xác suất ( được chỉ ra bằng cách đặt tích lũy thành 1).
Để làm ví dụ về cách hoạt động của hàm F.DIST.RT, giả sử bạn so sánh hai phương sai của mẫu, một bằng và một bằng. Điều này có nghĩa là giá trị f bằng. Ngoài ra, giả sử rằng cả hai mẫu đều đánh số 10 mục, có nghĩa là cả hai mẫu đều có bậc tự do bằng nhau và bạn muốn tính xác suất tích lũy. Công thức
= F.DIST.RT (2 / 4,9,9)
trả về giá trị 0,841761 cho thấy rằng có khoảng 84% xác suất mà bạn có thể quan sát thấy giá trị f lớn như thể phương sai của các mẫu là tương đương.
Hàm F.INV trả về giá trị f bên trái tương đương với xác suất phân phối f cho trước. Hàm sử dụng cú pháp
= F.INV (xác suất, deg_freedom1, deg_freedom2)
trong đó xác suất là xác suất của giá trị f mà bạn muốn tìm; deg_freedom1 là bậc tự do trong mẫu đầu tiên hoặc tử số; và deg_freedom2 là bậc tự do trong mẫu thứ hai hoặc mẫu số.
Hàm F.INV.RT trả về giá trị f bên phải tương đương với xác suất phân phối f cho trước. Hàm sử dụng cú pháp
= F.INV.RT (xác suất, deg_freedom1, deg_freedom2)
trong đó xác suất là xác suất của giá trị f mà bạn muốn tìm; deg_freedom1 là bậc tự do trong mẫu đầu tiên hoặc tử số; deg_freedom2 và là bậc tự do trong mẫu thứ hai hoặc mẫu số.
Hàm F.TEST so sánh phương sai của hai mẫu và trả về xác suất mà phương sai không khác nhau đáng kể. Hàm sử dụng cú pháp
= F.TEST (array1, array2)
trong đó array1 là phạm vi trang tính chứa mẫu đầu tiên và là phạm vi trang tính chứa mẫu thứ hai.
Để hiểu cách sử dụng hàm F.DIST, hãy xem xét một ví dụ:
Ví dụ
Giả sử chúng ta được cung cấp dữ liệu sau:
Để tìm ra xác suất F sử dụng hàm phân phối tích lũy, là đối số tích lũy TRUE, chúng ta sẽ sử dụng công thức sau:
Chúng tôi nhận được kết quả dưới đây:
Để tìm ra xác suất F bằng cách sử dụng hàm mật độ xác suất, là đối số tích lũy FALSE, chúng ta sẽ sử dụng công thức sau:
Chúng tôi nhận được kết quả dưới đây:
Các hàm hồi quy của Excel cho phép bạn thực hiện phân tích hồi quy hiệu quả. Hãy tìm hiểu những hàm quan trọng như FORECAST, INTERCEPT, và LINEST trong Excel để dự báo và phân tích dữ liệu.
Khi các macro Excel của bạn ngày càng trở nên mạnh mẽ và phức tạp, bạn có thể thấy rằng chúng giảm hiệu suất. Khi thảo luận về macro, từ hiệu suất thường đồng nghĩa với tốc độ. Tốc độ là tốc độ các thủ tục VBA của bạn thực hiện các tác vụ dự định của chúng. Sau đây là mười cách để giúp giữ cho macro Excel của bạn chạy ở mức hiệu suất tối ưu. Tạm dừng […]
Trước Excel 2007, các lập trình viên VBA đã sử dụng đối tượng CommandBar để tạo menu tùy chỉnh, thanh công cụ tùy chỉnh và menu phím tắt tùy chỉnh (nhấp chuột phải). Bắt đầu với Excel 2007, đối tượng CommandBar ở một vị trí khá kỳ lạ. Nếu bạn viết mã để tùy chỉnh menu hoặc thanh công cụ, Excel sẽ chặn mã đó và bỏ qua nhiều lệnh của bạn. Thay thế […]
Phân phối f là phân phối xác suất trong Excel so sánh tỷ lệ theo phương sai của các mẫu được lấy từ các quần thể khác nhau. Sự so sánh đó tạo ra một kết luận về việc liệu các phương sai trong các quần thể cơ bản có giống nhau hay không. F.DIST: Xác suất phân phối f bên trái Hàm F.DIST trả về xác suất bên trái của việc quan sát một tỷ lệ phương sai của hai mẫu càng lớn […]
Nếu bạn đã sử dụng bút hoặc bút tô sáng để vẽ trên các trang chiếu PowerPoint của mình trong khi trình bày, bạn có thể lưu các bản vẽ cho bản trình bày tiếp theo hoặc xóa chúng để lần sau khi trình chiếu, bạn sẽ bắt đầu với các trang chiếu PowerPoint sạch sẽ. Làm theo các hướng dẫn sau để xóa các bản vẽ bằng bút và bút tô sáng: Xóa từng đường một tại […]
Thư viện Kiểu chứa tệp CSS, tệp Ngôn ngữ biểu định kiểu mở rộng (XSL) và hình ảnh được sử dụng bởi các trang chính, bố cục trang và điều khiển được xác định trước trong SharePoint 2010. Để định vị tệp CSS trong thư viện Kiểu của trang xuất bản: Chọn Hành động trang → Xem Tất cả Nội dung Trang web. Nội dung của trang web xuất hiện. Thư viện Style nằm trong […]
Tìm hiểu cách sử dụng hàm XLOOKUP trong Excel 2016. Việc thay thế hàm VLOOKUP đơn giản và linh hoạt hơn đáng kể!
Đối với các vấn đề đơn giản, Bộ giải trong Excel thường nhanh chóng tìm ra các giá trị của biến Bộ giải tối ưu cho hàm mục tiêu. Tuy nhiên, trong một số trường hợp, Solver gặp khó khăn khi tìm các giá trị biến Solver tối ưu hóa hàm mục tiêu. Trong những trường hợp này, Solver thường hiển thị một thông báo hoặc một thông báo lỗi mô tả hoặc thảo luận về sự cố […]
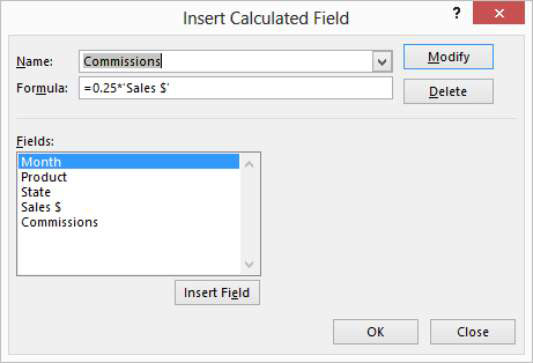
Bạn có thể dễ dàng xóa các trường và mục được tính toán khỏi bảng tổng hợp Excel. Để xóa trường được tính toán, hãy bấm vào một ô trong bảng tổng hợp. Sau đó nhấp vào lệnh Trường, Mục & Bộ của tab Phân tích và chọn Trường được Tính từ menu con xuất hiện. Khi Excel hiển thị hộp thoại Chèn Trường Tính toán, hãy chọn […]
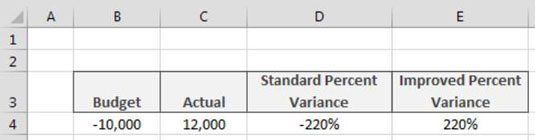
Công thức tính toán phần trăm phương sai trong Excel hoạt động hiệu quả trong hầu hết các trường hợp. Tuy nhiên, khi giá trị điểm chuẩn là một giá trị âm, công thức sẽ bị phá vỡ. Ví dụ, hãy tưởng tượng rằng bạn đang bắt đầu kinh doanh và dự kiến sẽ thua lỗ trong năm đầu tiên. Vì vậy, bạn cung cấp cho mình một ngân sách âm 10.000 đô la. Bây giờ hãy tưởng tượng rằng […]
