Comment normaliser les tableaux NumPy : un guide rapide

Si vous avez travaillé avec Python pour l'analyse de données ou l'apprentissage automatique, vous avez probablement rencontré des tableaux NumPy. Il s'agit d'un outil puissant pour gérer les données numériques, mais parfois, les données de ces tableaux doivent être ajustées ou « normalisées » pour être utilisées efficacement dans vos algorithmes. Mais que signifie normaliser un tableau ?

Pour normaliser un tableau NumPy, vous devez ajuster les valeurs du tableau afin qu'elles se situent dans une certaine plage, généralement entre 0 et 1, ou qu'elles aient une distribution normale standard avec une moyenne de 0 et un écart type de 1 Cela se fait souvent dans le domaine de l'apprentissage automatique et de l'analyse de données pour s'assurer que toutes les caractéristiques d'entrée ont la même échelle.

Dans cet article, nous allons explorer comment vous pouvez normaliser un tableau NumPy en Python. Nous examinerons les différentes méthodes que vous pouvez utiliser pour normaliser un tableau NumPy et examinerons également des exemples pour vous aider à mieux comprendre le concept.

Allons-y !

Table des matières

• Quelles sont les bases de la normalisation en Python ?
  • Qu'est-ce que la normalisation ?
  • Pourquoi la normalisation est-elle importante ?
  • Que sont les normes ?
  • Qu'est-ce que la normalisation dans l'apprentissage automatique ?
• Quelles sont les techniques de normalisation en Python ?
  • 1. Comment effectuer une mise à l'échelle min-max
  • 2. Comment effectuer la normalisation L1
  • 3. Comment effectuer la normalisation L2
• Comment utiliser Scikit-Learn pour la normalisation en Python
  • 1. Comment normaliser un tableau à l'aide de MinMaxScaler
  • 2. Comment effectuer une normalisation de ligne sur place
• Dernières pensées

Quelles sont les bases de la normalisation en Python ?

Avant d'implémenter la normalisation en Python, vous devez comprendre ce que signifie la normalisation.

Par conséquent, dans cette section, nous allons passer en revue ce qu'est la normalisation et ses concepts de base.

Qu'est-ce que la normalisation ?

La normalisation est un processus qui met à l'échelle et transforme les données en une plage normalisée. Cela se fait en divisant chaque élément des données par un paramètre. Le paramètre peut être la valeur maximale, la plage ou une autre norme.

Vous pouvez normaliser le tableau NumPy à l'aide de la norme euclidienne (également appelée norme L2). De plus, vous pouvez également normaliser les tableaux NumPy en redimensionnant les valeurs entre une certaine plage, généralement de 0 à 1.

En Python, la bibliothèque NumPy fournit un moyen efficace de normaliser les tableaux. Cela inclut également les tableaux et matrices multidimensionnels.

Pourquoi la normalisation est-elle importante ?

La normalisation est importante car elle garantit que les différentes caractéristiques sont traitées de la même manière lors de la comparaison et de l'analyse des données. Vous pouvez l'utiliser pour éliminer les biais ou les écarts potentiels qui pourraient survenir en raison des différentes échelles.

Que sont les normes ?

Le paramètre que vous utilisez pour la normalisation peut être différentes normes , telles que la norme euclidienne (L2), la norme Manhattan (L1) ou la norme max (L_inf). Vous utilisez des normes pour calculer la magnitude d'un vecteur ou d'une matrice . Ceux-ci sont ensuite utilisés comme facteur d'échelle pour normaliser les données.

Lorsque nous travaillons avec des matrices, nous utilisons souvent la norme de Frobenius , qui est une généralisation de la norme euclidienne pour les tableaux multidimensionnels.

L'exemple suivant montre la normalisation d'une matrice à l'aide de la norme de Frobenius :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
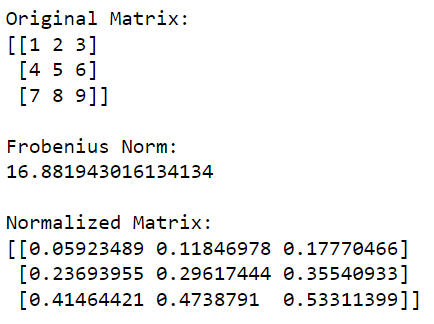
print(normalized_matrix)

Ce code Python importera d'abord la bibliothèque NumPy et l'utilisera pour créer une matrice. Il calcule ensuite la norme de Frobenius de la matrice puis divise chaque élément de la matrice par cette valeur pour la normaliser.

La sortie de ce code est donnée ci-dessous :

Qu'est-ce que la normalisation dans l'apprentissage automatique ?

Dans l'apprentissage automatique , la normalisation est une étape de prétraitement importante car elle améliore les performances des algorithmes.

Lors de l'exécution de techniques d'optimisation basées sur le gradient, vous constaterez que les fonctionnalités optimisées ont tendance à converger plus rapidement et plus efficacement. En effet, cela réduit le risque de mauvaise mise à l'échelle ou de gradients de disparition.

Quelles sont les techniques de normalisation en Python ?

Vous pouvez effectuer la normalisation des tableaux NumPy de plusieurs façons. Cependant, certaines méthodes sont plus populaires que d'autres en raison de leur grande efficacité.

Pour cette section, nous examinerons les trois techniques de normalisation largement utilisées :

1. Mise à l'échelle min-max

2. Normalisation L1

3. Normalisation L2

1. Comment effectuer une mise à l'échelle min-max

La mise à l'échelle min-max est également appelée normalisation linéaire ou mise à l'échelle des fonctionnalités. Dans la mise à l'échelle min-max, nous mettons à l'échelle les valeurs d'un tableau NumPy afin qu'elles se situent dans une plage spécifiée, généralement entre 0 et 1.

Pour ce faire, vous soustrayez la valeur minimale de chaque élément et divisez le résultat par la différence entre les valeurs maximale et minimale.

Vous pouvez représenter mathématiquement la mise à l'échelle min-max comme suit :

x' = (x - min(x)) / (max(x) - min(x))

L'exemple suivant montre comment effectuer une mise à l'échelle min-max à l'aide de la bibliothèque NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Ce code importera d'abord NumPy, puis calculera les valeurs minimale et maximale dans la matrice, qu'il mettra ensuite à l'échelle de sorte que toutes les valeurs soient comprises entre 0 (correspondant à la valeur minimale d'origine) et 1 (correspondant à la valeur maximale d'origine).

La sortie de ce code est donnée ci-dessous :

La mise à l'échelle min-max est une forme de mise à l'échelle très courante dans l'apprentissage automatique et le prétraitement des données.

2. Comment effectuer la normalisation L1

La normalisation L1 utilise la norme L1, qui est la somme des valeurs absolues des éléments du tableau. Ceci est particulièrement utile pour les matrices creuses. Il garantit que la somme des valeurs absolues des éléments de tableau normalisés est égale à 1.

La formule de normalisation L1 est :

x' = x / sum(|x|)

L'exemple suivant montre comment effectuer la normalisation L1 à l'aide de NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
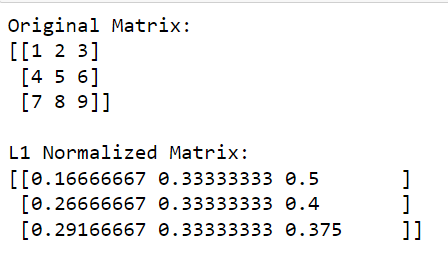
print(l1_normalized_matrix)

Dans ce code, np.linalg.norm (matrix, 1, axis=1, keepdims=True) calcule la norme L1 pour chaque ligne (ceci est fait en spécifiant axis=1).

Cette opération renverra un vecteur colonne où chaque élément est la norme L1 de la ligne correspondante. En divisant la matrice d'origine par ces normes (en effectuant la division élément par élément), nous obtenons la version normalisée L1 de la matrice.

La sortie est donnée ci-dessous :

3. Comment effectuer la normalisation L2

La normalisation L2 utilise la norme L2, qui est la racine carrée de la somme des éléments du tableau au carré.

Cette méthode convertit le tableau normalisé en un vecteur unitaire avec une norme 2 de 1. La normalisation L2 est utile pour la réduction dimensionnelle et garantit une importance égale pour toutes les caractéristiques.

La formule de normalisation L2 est :

x' = x / sqrt(sum(x^2))

Voici comment effectuer la normalisation L2 à l'aide de NumPy :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
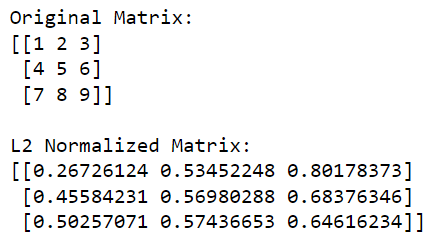
print(l2_normalized_matrix)

Dans ce code, np.linalg.norm(matrix, 2, axis=1, keepdims=True) calcule la norme L2 (norme euclidienne) pour chaque ligne (cela se fait en spécifiant axis=1). Cette opération renverra un vecteur colonne où chaque élément est la norme L2 de la ligne correspondante.

En divisant la matrice d'origine par ces normes (en effectuant la division élément par élément), nous obtenons la version normalisée L2 de la matrice.

La sortie est donnée ci-dessous :

Très bien, maintenant que nous avons passé en revue les méthodes courantes de création d'un tableau normalisé à l'aide de NumPy, examinons comment vous pouvez faire de même avec d'autres bibliothèques Python dans la section suivante.

Comment utiliser Scikit-Learn pour la normalisation en Python

Scikit-learn est une puissante bibliothèque Python pour l'apprentissage automatique. Il fournit plusieurs outils pour le prétraitement des données.

Un outil que vous pouvez utiliser est le module sklearn.preprocessing , qui propose diverses techniques pour effectuer la normalisation. Il existe de nombreuses fonctions de mise à l'échelle, de transformateurs et de normalisateurs différents. Cependant, nous nous concentrerons sur MinMaxScaler et la fonction normalize .

Pour prétraiter les données avec scikit-learn, vous utilisez principalement l'API transformer. Cela inclut les méthodes fit , transform et fit_transform .

1. Comment normaliser un tableau à l'aide de MinMaxScaler

Le MinMaxScaler est un scaler qui normalise les données dans une plage spécifiée, généralement [0, 1].

La formule pour MinMaxScalar est donnée ci-dessous :

scaled_value = (value - min_value) / (max_value - min_value)

Pour implémenter le MinMaxScaler , vous pouvez suivre ces étapes :

1. Importez les bibliothèques requises :

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Créez un tableau NumPy :

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Instanciez le MinMaxScaler et adaptez-le aux données :

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Transformez les données à l'aide de la méthode transform ou fit_transform :

   normalized_data = scaler.transform(data)

La sortie de ce code est donnée ci-dessous :

Comme vous pouvez le voir dans la sortie, MinMaxScalarMatrix n'a que des valeurs comprises entre 0 et 1.

2. Comment effectuer une normalisation de ligne sur place

Vous pouvez également utiliser la normalisation de ligne sur place comme alternative, en utilisant la fonction de normalisation .

Cette méthode normalise chaque tableau ou caractéristique d'entrée indépendamment en mettant à l'échelle le vecteur selon une norme unitaire. Par défaut, la fonction de normalisation utilise la norme L2 pour effectuer une normalisation simple, mais vous pouvez choisir d'autres options de norme.

L'exemple suivant illustre la normalisation de lignes sur place :

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
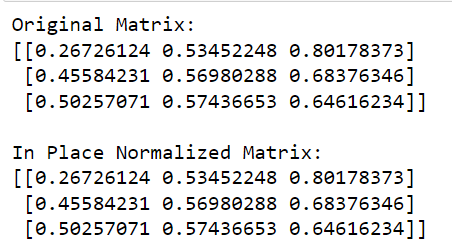
print(matrix)

Dans ce code, nous appelons la fonction normalize de sklearn , définissons la norme à utiliser ("l2" dans ce cas) et définissons copy=False pour effectuer une normalisation sur place.

La sortie de ce code est donnée ci-dessous :

Pour en savoir plus sur l'apprentissage automatique en Python , regardez la vidéo suivante :

Dernières pensées

Au fur et à mesure que vous explorez la science des données et l'apprentissage automatique, vous constaterez que le processus de normalisation est une étape essentielle de votre pipeline de prétraitement des données.

Tout d'abord, il place des caractéristiques différentes sur une échelle commune. Cela rend vos modèles moins sensibles à l'échelle des entrées. Il peut grandement améliorer les performances de nombreux algorithmes d'apprentissage automatique.

Deuxièmement, il vous aide à accélérer le processus de formation. Certains algorithmes, en particulier ceux basés sur des calculs de distance calculés, convergent plus rapidement lorsque les données sont normalisées.

En apprenant à normaliser les données, vous vous dotez d'une compétence cruciale. La normalisation est un outil pratique utilisé couramment dans les applications du monde réel. Cela vous aidera à réduire la probabilité de résultats inattendus dus à des valeurs aberrantes ou à des différences d'unités.

Comme tout outil, la clé de la maîtrise de la normalisation réside dans la pratique. Alors, n'hésitez pas à vous salir les mains et à expérimenter différents ensembles de données et valeurs aléatoires. Le monde de la science des données est votre huître. Bon codage !