NumPy 배열을 정규화하는 방법: 빠른 안내서

데이터 분석 또는 기계 학습을 위해 Python으로 작업한 적이 있다면 NumPy 배열을 접했을 가능성이 큽니다. 이들은 숫자 데이터를 처리하기 위한 강력한 도구이지만 때로는 알고리즘에서 효과적으로 사용하기 위해 이러한 배열 내의 데이터를 조정하거나 '정규화'해야 합니다. 그러나 배열을 정규화한다는 것은 무엇을 의미합니까?

NumPy 배열을 정규화하려면 일반적으로 0과 1 사이의 특정 범위에 속하거나 평균이 0이고 표준 편차가 1인 표준 정규 분포를 갖도록 배열의 값을 조정해야 합니다. 이는 모든 입력 기능이 동일한 척도를 갖도록 하기 위해 기계 학습 및 데이터 분석 분야에서 종종 수행됩니다.

이 기사에서는 Python에서 NumPy 배열을 정규화하는 방법을 살펴봅니다. NumPy 배열을 정규화하는 데 사용할 수 있는 다양한 방법을 살펴보고 개념을 더 잘 이해하는 데 도움이 되는 예제도 살펴보겠습니다.

그것에 들어가자!

목차

• Python에서 정규화의 기본 사항은 무엇입니까?
  • 정규화란 무엇입니까?
  • 정규화가 중요한 이유는 무엇입니까?
  • 규범이란 무엇입니까?
  • 기계 학습에서 정규화란 무엇입니까?
• Python의 정규화 기술은 무엇입니까?
  • 1. Min-Max 스케일링 방법
  • 2. L1 정규화 수행 방법
  • 3. L2 정규화 수행 방법
• Python에서 정규화를 위해 Scikit-Learn을 사용하는 방법
  • 1. MinMaxScaler를 사용하여 배열을 정규화하는 방법
  • 2. 내부 행 정규화를 수행하는 방법
• 마지막 생각들

Python에서 정규화의 기본 사항은 무엇입니까?

Python에서 정규화를 구현하기 전에 정규화가 무엇을 의미하는지 이해해야 합니다.

따라서 이 섹션에서는 정규화와 그 핵심 개념에 대해 살펴보겠습니다.

정규화란 무엇입니까?

정규화는 데이터를 표준화된 범위로 확장 하고 변환하는 프로세스입니다 . 이는 데이터의 각 요소를 매개 변수로 나누어 수행됩니다. 매개변수는 최대값, 범위 또는 기타 규범이 될 수 있습니다.

유클리드 표준(L2 표준이라고도 함)을 사용하여 NumPy 배열을 정규화할 수 있습니다. 또한 특정 범위(일반적으로 0에서 1 사이) 사이의 값을 재조정하여 NumPy 배열을 정규화할 수도 있습니다.

Python에서 NumPy 라이브러리는 배열을 정규화하는 효율적인 방법을 제공합니다. 여기에는 다차원 배열과 행렬도 포함됩니다.

정규화가 중요한 이유는 무엇입니까?

정규화는 데이터를 비교하고 분석할 때 서로 다른 기능이 동일하게 처리되도록 하기 때문에 중요합니다. 다양한 척도로 인해 발생할 수 있는 잠재적 편향이나 불일치를 제거하는 데 사용할 수 있습니다.

규범이란 무엇입니까?

정규화에 사용하는 매개변수는 유클리드 노름(L2), 맨해튼 노름(L1) 또는 최대 노름(L_inf)과 같은 다른 노름 일 수 있습니다. 규범을 사용하여 벡터 또는 행렬 의 크기를 계산합니다 . 그런 다음 데이터를 정규화하기 위한 배율 인수로 사용됩니다.

행렬로 작업할 때 다차원 배열에 대한 유클리드 표준의 일반화인 Frobenius 표준을 자주 사용합니다 .

다음 예는 Frobenius 노름을 사용한 행렬의 정규화를 보여줍니다.

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
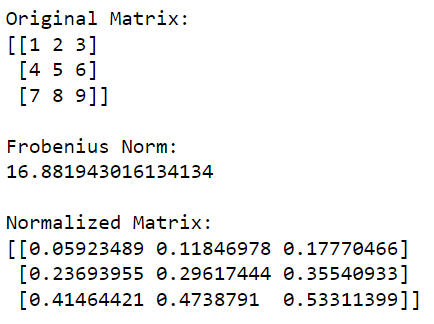
print(normalized_matrix)

이 Python 코드는 먼저 NumPy 라이브러리를 가져오고 이를 사용하여 행렬을 만듭니다. 그런 다음 행렬의 Frobenius 노름을 계산한 다음 행렬의 각 요소를 이 값으로 나누어 정규화합니다.

이 코드의 출력은 다음과 같습니다.

기계 학습에서 정규화란 무엇입니까?

기계 학습 에서 정규화는 알고리즘의 성능을 향상시키기 때문에 중요한 전처리 단계입니다.

그래디언트 기반 최적화 기술을 수행할 때 최적화된 기능이 더 빠르고 효율적으로 수렴되는 경향이 있음을 알 수 있습니다. 이는 스케일링 불량 또는 그라데이션 소실의 위험을 줄이기 때문입니다.

Python의 정규화 기술은 무엇입니까?

여러 가지 방법으로 NumPy 배열 의 정규화를 수행할 수 있습니다 . 그러나 일부 방법은 효율성이 높기 때문에 다른 방법보다 더 많이 사용됩니다.

이 섹션에서는 널리 사용되는 세 가지 정규화 기술을 살펴보겠습니다.

1. 최소-최대 스케일링

2. L1 정규화

3. L2 정규화

1. Min-Max 스케일링 방법

최소-최대 스케일링은 선형 정규화 또는 기능 스케일링이라고도 합니다. 최소-최대 스케일링에서는 NumPy 배열의 값을 지정된 범위(일반적으로 0과 1 사이)에 포함되도록 스케일링합니다.

이렇게 하려면 각 요소에서 최소값을 빼고 그 결과를 최대값과 최소값의 차이로 나눕니다.

최소-최대 스케일링을 수학적으로 다음과 같이 나타낼 수 있습니다.

x' = (x - min(x)) / (max(x) - min(x))

다음 예제는 NumPy 라이브러리를 사용하여 최소-최대 크기 조정을 수행하는 방법을 보여줍니다.

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

이 코드는 먼저 NumPy를 가져온 다음 행렬의 최소값과 최대값을 계산한 다음 모든 값이 0(원래 최소값에 해당)과 1(원래 최대값에 해당) 사이가 되도록 확장합니다.

이 코드의 출력은 다음과 같습니다.

최소-최대 스케일링은 기계 학습 및 데이터 전처리에서 매우 일반적인 스케일링 형식입니다.

2. L1 정규화 수행 방법

L1 정규화는 배열 요소의 절대값의 합인 L1-norm을 사용합니다. 이는 희소 행렬에 특히 유용합니다. 정규화된 배열 요소의 절대값 합계가 1이 되도록 합니다.

L1 정규화 공식은 다음과 같습니다.

x' = x / sum(|x|)

다음 예제는 NumPy를 사용하여 L1 정규화를 수행하는 방법을 보여줍니다.

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
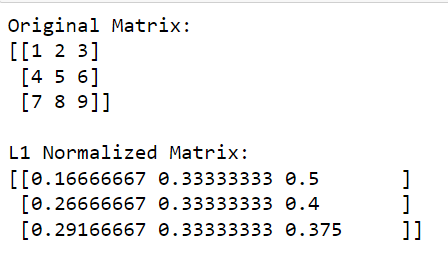
print(l1_normalized_matrix)

이 코드에서 np.linalg.norm (matrix, 1, axis=1, keepdims=True)은 각 행에 대한 L1 표준을 계산합니다(이는 axis=1을 지정하여 수행됨).

이 작업은 각 요소가 해당 행의 L1 표준인 열 벡터를 반환합니다. 원래 행렬을 이러한 규범으로 나누면(요소별로 나누기 수행) 행렬의 L1 정규화 버전을 얻습니다.

출력은 다음과 같습니다.

3. L2 정규화 수행 방법

L2 정규화는 제곱 배열 요소 합계의 제곱근인 L2-norm을 사용합니다.

이 방법은 정규화된 배열을 2-노름이 1인 단위 벡터로 변환합니다. L2 정규화는 차원 축소에 유용하며 모든 기능에 대해 동일한 중요도를 보장합니다.

L2 정규화 공식은 다음과 같습니다.

x' = x / sqrt(sum(x^2))

다음은 NumPy를 사용하여 L2 정규화를 수행하는 방법입니다 .

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
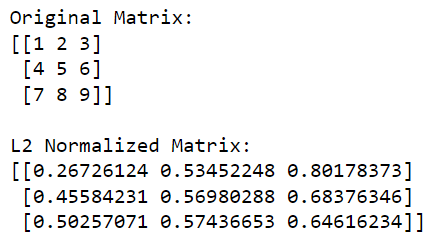
print(l2_normalized_matrix)

이 코드에서 np.linalg.norm(matrix, 2, axis=1, keepdims=True) 는 각 행에 대한 L2 노름(유클리드 노름)을 계산합니다(이는 axis=1을 지정하여 수행됨). 이 작업은 각 요소가 해당 행의 L2 표준인 열 벡터를 반환합니다.

원래 행렬을 이러한 규범으로 나누면(요소별로 나누기 수행) 행렬의 L2 정규화 버전을 얻습니다.

출력은 다음과 같습니다.

자, 이제 NumPy를 사용하여 정규화된 배열을 만드는 인기 있는 방법을 살펴보았으므로 다음 섹션에서 다른 Python 라이브러리를 사용하여 동일한 작업을 수행하는 방법을 살펴보겠습니다.

Python에서 정규화를 위해 Scikit-Learn을 사용하는 방법

Scikit-learn은 기계 학습을 위한 강력한 Python 라이브러리입니다. 데이터 전처리를 위한 여러 도구를 제공합니다.

사용할 수 있는 한 가지 도구는 정규화를 수행하는 다양한 기술을 제공하는 sklearn.preprocessing 모듈입니다. 다양한 스케일러 기능, 변환기 및 노멀라이저를 사용할 수 있습니다. 그러나 MinMaxScaler 와 정규화 기능 에 초점을 맞출 것입니다 .

scikit-learn으로 데이터를 전처리하기 위해 주로 변환기 API를 사용합니다. 여기에는 fit , transform 및 fit_transform 메서드가 포함됩니다.

1. MinMaxScaler를 사용하여 배열을 정규화하는 방법

MinMaxScaler는 데이터 를 지정된 범위(일반적으로 [0, 1])로 정규화하는 스케일러입니다.

MinMaxScalar의 공식은 다음과 같습니다.

scaled_value = (value - min_value) / (max_value - min_value)

MinMaxScaler 를 구현하려면 다음 단계를 따르십시오.

1. 필요한 라이브러리를 가져옵니다.

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. NumPy 배열을 만듭니다.

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. MinMaxScaler 를 인스턴스화 하고 데이터에 맞춥니다.

   scaler = MinMaxScaler()
   scaler.fit(data)

4. transform 또는 fit_transform 메서드를 사용하여 데이터를 변환합니다 .

   normalized_data = scaler.transform(data)

이 코드의 출력은 다음과 같습니다.

출력에서 볼 수 있듯이 MinMaxScalarMatrix에는 0에서 1 사이의 값만 있습니다.

2. 내부 행 정규화를 수행하는 방법

normalize 함수 를 사용하여 내부 행 정규화를 대안으로 사용할 수도 있습니다 .

이 방법은 벡터를 단위 표준으로 크기 조정하여 각 입력 배열 또는 기능을 독립적으로 정규화합니다. 기본적으로 정규화 기능은 L2 표준을 사용하여 간단한 정규화를 수행하지만 다른 표준 옵션을 선택할 수 있습니다.

다음 예제는 인플레이스 행 정규화를 보여줍니다.

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
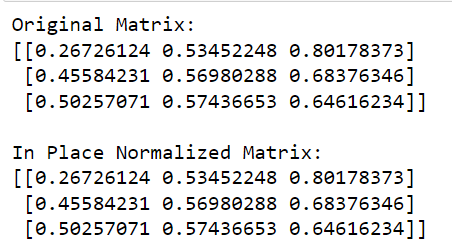
print(matrix)

이 코드에서는 sklearn 에서 normalize 함수를 호출하고 , 사용할 규범(이 경우 'l2')을 정의하고, 내부 정규화를 수행하도록 copy=False를 설정합니다.

이 코드의 출력은 다음과 같습니다.

Python 의 기계 학습에 대해 자세히 알아보려면 다음 비디오를 확인하십시오.

마지막 생각들

데이터 과학 및 머신 러닝을 자세히 살펴보면 정규화 프로세스가 데이터 전처리 파이프라인의 필수 단계임을 알게 될 것입니다.

첫째, 공통 척도에 서로 다른 기능을 배치합니다. 이렇게 하면 모델이 입력 규모에 덜 민감해집니다. 많은 기계 학습 알고리즘의 성능을 크게 향상시킬 수 있습니다.

둘째, 교육 과정의 속도를 높이는 데 도움이 됩니다. 일부 알고리즘, 특히 계산된 거리 계산을 기반으로 하는 알고리즘은 데이터가 정규화될 때 더 빠르게 수렴됩니다.

데이터를 정규화하는 방법을 배우면 중요한 기술을 갖추게 됩니다. 정규화는 실제 응용 프로그램에서 일상적으로 사용되는 실용적인 도구입니다. 이상치 또는 단위 차이로 인해 예상치 못한 결과가 발생할 가능성을 줄이는 데 도움이 됩니다.

다른 도구와 마찬가지로 정규화를 마스터하는 열쇠는 실제로 있습니다. 따라서 주저하지 말고 손을 더럽히고 다양한 데이터 세트와 임의의 값을 실험해 보십시오. 데이터 과학 의 세계는 당신의 굴입니다. 즐거운 코딩하세요!