Streudiagramm-Visualisierungen mit Charticulator

In diesem Tutorial erfahren Sie, wie Sie mit Charticulator eine Streudiagramm-Visualisierung für Ihren LuckyTemplates-Bericht erstellen und entwerfen.
Pi ist eine grundlegende mathematische Konstante, die das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser darstellt. Die Nutzung von Pi in Python ist bei geometrischen Berechnungen, Trigonometrie und verschiedenen anderen mathematischen Operationen unerlässlich.
Python bietet mehrere Möglichkeiten, auf Pi zuzugreifen und es in Berechnungen zu verwenden. Die Math- und NumPy-Bibliotheken sind zwei häufig verwendete Module, die Pi als Konstante bereitstellen.
Es gibt mehrere andere Module, die die Konstante bereitstellen. Ihre Wahl hängt davon ab, wie viel mathematische Präzision Sie benötigen und welche anderen Berechnungen Ihre Anwendung erfordert.
Dieser Artikel zeigt Ihnen, wie Sie mit vier Methoden auf Pi zugreifen und erklärt, welche Ihren Anforderungen am besten entspricht.
Lassen Sie uns eintauchen.
Inhaltsverzeichnis
Pi in Python verstehen

Pi (?) stellt das Verhältnis des Kreisumfangs (c) zu seinem Durchmesser (d) dar. Einfacher ausgedrückt: ? = c/d.
Der Wert von Pi beträgt ungefähr 3,14159.
Pi ist eine irrationale Zahl, das heißt, sie geht unendlich weiter, ohne sich zu wiederholen. Er kann nicht als einfacher Bruch ausgedrückt werden und es gibt keine exakte Dezimaldarstellung.
Hier sind die ersten paar Ziffern von Pi, um Ihnen eine Vorstellung von seiner Natur zu geben:
3.14159265358979323846...Der Wert von Pi wird in Berechnungen aus praktischen Gründen oft auf wenige Dezimalstellen gekürzt, beispielsweise 3,14 oder 22/7.
Allerdings ist diese verkürzte Darstellung für einige Anwendungen möglicherweise nicht genau genug, beispielsweise für hochpräzise numerische Simulationen oder bestimmte mathematische Beweise.
4 gängige Möglichkeiten, in Python auf Pi zuzugreifen

Die vier häufigsten Möglichkeiten, in Python auf ein Pi zuzugreifen, sind:
Mathematikmodul
NumPy-Modul
SciPy-Modul
cmath-Modul
Bedenken Sie, dass die math.pi- Konstante von Python zwar für die meisten Zwecke genau genug ist, dass aber in anderen Bibliotheken sogar noch genauere Näherungen verfügbar sind. NumPy bietet beispielsweise ein höheres Maß an Präzision.
Die Wahl der zu verwendenden Bibliothek hängt von Ihren spezifischen Anforderungen und anderen Funktionalitäten ab, die Sie möglicherweise von der Bibliothek benötigen. Wenn Sie in Ihrem Projekt bereits NumPy oder SciPy verwenden , wäre es sinnvoll, deren jeweilige Pi-Konstanten zu verwenden.
Wenn Sie mit komplexen Zahlen arbeiten müssen, ist das cmath- Modul die beste Wahl.
Wenn Sie keine zusätzlichen Funktionen dieser Bibliotheken benötigen und nur einen ungefähren Wert von Pi benötigen, ist die Verwendung der integrierten Mathematikbibliothek von Python wahrscheinlich die beste Option.
So greifen Sie mit der Mathematikbibliothek auf Pi zu
Das Mathematikmodul in Python ermöglicht die Arbeit mit der Zahl Pi und liefert eine genaue Näherung mit bis zu 15 Dezimalstellen.
Dies ist eines der integrierten Module von Python, was bedeutet, dass Sie es nicht separat herunterladen und installieren müssen.
Sie haben zwei Möglichkeiten, Pi zur Verwendung in Ihrem Code zu importieren:
Mathematikbibliothek importieren
Importieren Sie nur die Pi-Konstante
Dieser Code importiert die vollständige Bibliothek:
import math
pi_value = math.piDieser Code importiert nur die Pi-Konstante:
from math import pi
pi_value = pi3 Möglichkeiten, die Pi-Konstante mit anderen mathematischen Funktionen zu verwenden
Neben der Pi-Konstante bietet das Mathematikmodul viele weitere mathematische Funktionen. Diese Funktionen können mit math.pi kombiniert werden , um:
Berechnen Sie den Umfang eines Kreises
Berechnen Sie die Fläche eines Kreises
Berechnen Sie Bogenmaß und Grad
Schauen wir uns die einzelnen Elemente der Reihe nach an.
1. Umfang eines Kreises

Der Umfang eines Kreises kann mit der folgenden Formel berechnet werden:
C = 2 ? R
C ist der Umfang
? ist die Konstante Pi
r ist der Radius des Kreises.
In Python können Sie den Umfang eines Kreises berechnen, indem Sie das Mathematikmodul importieren und die mathematische Konstante pi wie folgt verwenden:
import math
radius = 5
circumference = 2 * math.pi * radius
print(circumference)Möglicherweise möchten Sie auch den euklidischen Abstand für zwei Punkte auf dem Umfang ermitteln. Dieses Video zeigt die Berechnungen:
2. Fläche eines Kreises
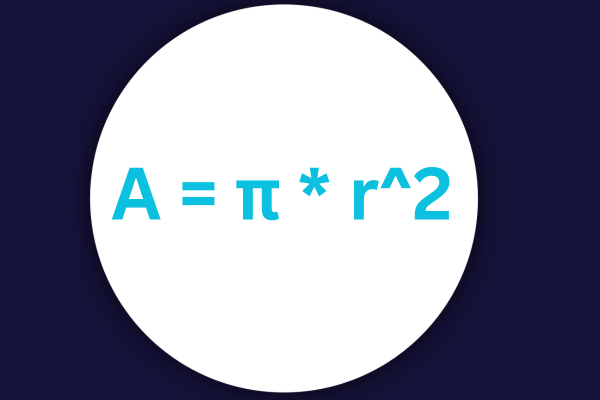
Die Fläche eines Kreises kann mit der folgenden Formel berechnet werden:
A = ? * r^2
A ist die Fläche
? ist die Konstante Pi
r ist der Radius des Kreises.
In Python können Sie die Fläche eines Kreises wie folgt berechnen:
import math
radius = 5
area = math.pi * (radius ** 2)
print(area)3. Bogenmaß und Grad

Winkel können in zwei gängigen Einheiten gemessen werden: Grad und Bogenmaß . Ein Vollkreis umfasst 360 Grad oder 2? Bogenmaß. Um Grad in Bogenmaß umzurechnen, können Sie Pi in einer einfachen Formel verwenden:
Bogenmaß = Grad * (? / 180)
Das Mathematikmodul bietet jedoch auch eine praktische Funktion zur Umrechnung von Grad in Bogenmaß: die math.radians() . Dies vereinfacht Ihre Berechnungen.
Hier ist ein einfaches Beispiel für die Verwendung der Funktion radians() :
import math
angle_degrees = 45
angle_radians = math.radians(angle_degrees)
print(angle_radians)Die Funktion gibt die Berechnung basierend auf der integrierten mathematischen Pi-Konstante zurück.
So verwenden Sie Pi mit dem NumPy-Modul
NumPy ist eine beliebte Python-Bibliothek für die Arbeit mit numerischen Daten. Es liefert eine Konstante für die mathematische Konstante pi (ungefähr 3,14159).
Im Gegensatz zur Mathematikbibliothek ist NumPy kein integriertes Python-Modul. Sie können es mit pip, dem Paketmanager von Python, installieren. Der Befehl zum Installieren von Python NumPy wäre normalerweise:
pip install numpyHier ist ein Beispiel für den Import des Moduls und den Zugriff auf die pi NumPy-Konstante:
import numpy as np
pi_value = np.pi
print(pi_value)Dieser Code gibt den Wert der pi-Variablen (3.141592653589793) aus der NumPy-Bibliothek aus.
So verwenden Sie Pi mit dem SciPy-Modul
SciPy ist eine weitere weit verbreitete Python-Bibliothek für wissenschaftliche und technische Berechnungen. Es baut auf der NumPy-Bibliothek auf und umfasst mehrere zusätzliche Funktionen.
Sie können es mit pip, dem Paketmanager von Python, installieren. Der Befehl zum Installieren von SciPy wäre normalerweise:
pip install scipyHier ist ein Beispiel für den Import von SciPy und den Zugriff auf die Pi-Konstante:
import scipy
pi_value = scipy.pi
print(pi_value)Dieser Code gibt den von der SciPy-Bibliothek bereitgestellten Wert von pi (3.141592653589793) zurück.
So verwenden Sie komplexe Zahlen mit dem cmath-Modul
Python bietet über das integrierte cmath- Modul Unterstützung für komplexe Zahlen.
Hier ist ein Beispiel für die Verwendung der Pi-Konstante im cmath- Modul für Berechnungen mit komplexen Zahlen:
import cmath
# Define a complex number
z = 1 + 1j
# Compute the power of pi using the complex number
result = cmath.exp(z * cmath.pi)
print(result) # Output: (-1-2.8421709430404007e-14j)
Fehler- und Ausnahmebehandlung mit Pi in Python

Bei der Durchführung von Berechnungen mit pi in Python empfiehlt es sich immer, geeignete Techniken zur Ausnahmebehandlung zu verwenden. Möglicherweise treten einige der häufigsten Berechnungsfehler auf:
ZeroDivisionError
Überlauffehler
ArithmeticError
Um mehrere Ausnahmen zu behandeln, können Sie die Anweisungen „try“, „except“ und „finally“ in Python verwenden :
try:
# Perform calculation here
except (ZeroDivisionError, OverflowError, ArithmeticError):
# Handle specific errors here
finally:
# Code to be executed regardless of any exceptions
Hier ist ein Beispiel für den Umgang mit Fehlern bei der Berechnung der Kreisfläche:
import math
def calculate_area(r):
pi = math.pi
try:
area = pi * r**2
except (TypeError, OverflowError, ValueError):
area = None
print("Error: Invalid input or calculation failure")
finally:
return area
radius = 5
circle_area = calculate_area(radius)
print(circle_area)
Abschließende Gedanken
Sie haben gelernt, wie Sie mit vier verschiedenen Python-Modulen auf Pi zugreifen. Wählen Sie je nach Ihren Anforderungen unbedingt diejenige aus, die die von Ihnen benötigte Genauigkeit bietet.
Die vielen Beispiele in diesem Artikel decken die meisten Szenarien ab, denen Sie bei Ihren mathematischen Berechnungen begegnen werden. Wenn Sie weitere Hilfe benötigen, sind unser Python-Spickzettel und ChatGPT großartige Ressourcen.
Viel Spaß beim Codieren!
In diesem Tutorial erfahren Sie, wie Sie mit Charticulator eine Streudiagramm-Visualisierung für Ihren LuckyTemplates-Bericht erstellen und entwerfen.
Erfahren Sie, wie Sie ein PowerApps-Suchfeld von Grund auf erstellen und es an das Gesamtthema Ihrer App anpassen.
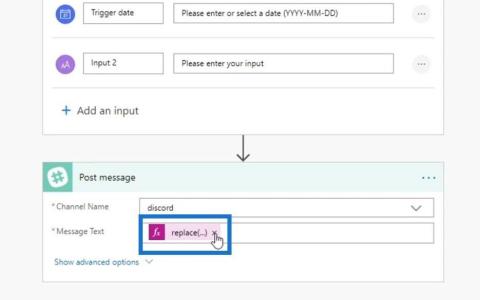
Erlernen Sie ganz einfach zwei komplizierte Power Automate String-Funktionen, die in Microsoft Flows verwendet werden können – die Funktionen substring und indexOf.
Dieses Tutorial konzentriert sich auf die Power Query M-Funktion „number.mod“, um ein abwechselndes 0-1-Muster in der Datumstabelle zu erstellen.
In diesem Tutorial führe ich eine Prognosetechnik durch, bei der ich meine tatsächlichen Ergebnisse mit meinen Prognosen vergleiche und sie kumulativ betrachte.
In diesem Blog erfahren Sie, wie Sie mit Power Automate E-Mail-Anhänge automatisch in SharePoint speichern und E-Mails anschließend löschen.
Erfahren Sie, wie die Do Until Schleifensteuerung in Power Automate funktioniert und welche Schritte zur Implementierung erforderlich sind.
In diesem Tutorial erfahren Sie, wie Sie mithilfe der ALLSELECTED-Funktion einen dynamischen gleitenden Durchschnitt in LuckyTemplates berechnen können.
Durch diesen Artikel erhalten wir ein klares und besseres Verständnis für die dynamische Berechnung einer laufenden oder kumulativen Gesamtsumme in LuckyTemplates.
Erfahren und verstehen Sie die Bedeutung und ordnungsgemäße Verwendung der Power Automate-Aktionssteuerung „Auf jede anwenden“ in unseren Microsoft-Workflows.