So normalisieren Sie NumPy-Arrays: Eine Kurzanleitung

Wenn Sie mit Python für Datenanalysen oder maschinelles Lernen gearbeitet haben, sind Sie wahrscheinlich schon auf NumPy-Arrays gestoßen. Sie sind ein leistungsstarkes Werkzeug für den Umgang mit numerischen Daten. Manchmal müssen die Daten in diesen Arrays jedoch angepasst oder „normalisiert“ werden, um effektiv in Ihren Algorithmen verwendet zu werden. Aber was bedeutet es, ein Array zu normalisieren?

Um ein NumPy-Array zu normalisieren, müssen Sie die Werte im Array so anpassen, dass sie in einen bestimmten Bereich fallen, normalerweise zwischen 0 und 1, oder dass sie eine Standardnormalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1 aufweisen Dies geschieht häufig im Bereich des maschinellen Lernens und der Datenanalyse, um sicherzustellen, dass alle Eingabemerkmale den gleichen Maßstab haben.

In diesem Artikel untersuchen wir, wie Sie ein NumPy-Array in Python normalisieren können. Wir werden uns die verschiedenen Methoden ansehen, mit denen Sie ein NumPy-Array normalisieren können, und sehen uns auch Beispiele an, die Ihnen helfen, das Konzept besser zu verstehen.

Lasst uns loslegen!

Inhaltsverzeichnis

• Was sind die Grundlagen der Normalisierung in Python?
  • Was ist Normalisierung?
  • Warum ist Normalisierung wichtig?
  • Was sind Normen?
  • Was ist Normalisierung beim maschinellen Lernen?
• Was sind die Normalisierungstechniken in Python?
  • 1. So führen Sie eine Min-Max-Skalierung durch
  • 2. So führen Sie die L1-Normalisierung durch
  • 3. So führen Sie eine L2-Normalisierung durch
• So verwenden Sie Scikit-Learn zur Normalisierung in Python
  • 1. So normalisieren Sie ein Array mit MinMaxScaler
  • 2. So führen Sie eine In-Place-Zeilennormalisierung durch
• Abschließende Gedanken

Was sind die Grundlagen der Normalisierung in Python?

Bevor wir die Normalisierung in Python implementieren, müssen Sie verstehen, was Normalisierung bedeutet.

Daher gehen wir in diesem Abschnitt darauf ein, was Normalisierung und ihre Kernkonzepte sind.

Was ist Normalisierung?

Normalisierung ist ein Prozess, der Daten skaliert und in einen standardisierten Bereich umwandelt . Dies geschieht, indem jedes Element der Daten durch einen Parameter dividiert wird. Der Parameter kann der Maximalwert, der Bereich oder eine andere Norm sein.

Sie können das NumPy-Array mithilfe der euklidischen Norm (auch als L2-Norm bekannt) normalisieren. Darüber hinaus können Sie NumPy-Arrays auch normalisieren, indem Sie die Werte innerhalb eines bestimmten Bereichs, normalerweise 0 bis 1, neu skalieren.

In Python bietet die NumPy-Bibliothek eine effiziente Möglichkeit, Arrays zu normalisieren. Dazu gehören auch mehrdimensionale Arrays und Matrizen.

Warum ist Normalisierung wichtig?

Die Normalisierung ist wichtig, da sie sicherstellt, dass unterschiedliche Merkmale beim Vergleich und der Analyse von Daten gleich behandelt werden. Sie können damit potenzielle Verzerrungen oder Diskrepanzen beseitigen, die aufgrund unterschiedlicher Maßstäbe auftreten können.

Was sind Normen?

Der Parameter, den Sie für die Normalisierung verwenden, kann verschiedene Normen sein , beispielsweise die Euklidische Norm (L2), die Manhattan-Norm (L1) oder die Max-Norm (L_inf). Sie verwenden Normen, um die Größe eines Vektors oder einer Matrix zu berechnen . Diese werden dann als Skalierungsfaktor zur Normalisierung der Daten verwendet.

Bei der Arbeit mit Matrizen verwenden wir häufig die Frobenius-Norm , eine Verallgemeinerung der euklidischen Norm für mehrdimensionale Arrays.

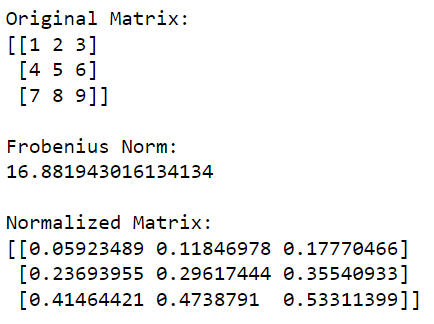
Das folgende Beispiel zeigt die Normalisierung einer Matrix mithilfe der Frobenius-Norm:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')

# Normalize the matrix
normalized_matrix = matrix / frobenius_norm

print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
print(normalized_matrix)

Dieser Python-Code importiert zunächst die NumPy-Bibliothek und verwendet sie zum Erstellen einer Matrix. Anschließend berechnet es die Frobenius-Norm der Matrix und dividiert anschließend jedes Element in der Matrix durch diesen Wert, um ihn zu normalisieren.

Die Ausgabe dieses Codes ist unten angegeben:

Was ist Normalisierung beim maschinellen Lernen?

Beim maschinellen Lernen ist die Normalisierung ein wichtiger Vorverarbeitungsschritt, da sie die Leistung von Algorithmen verbessert.

Bei der Durchführung von Gradienten-basierten Optimierungstechniken werden Sie feststellen, dass optimierte Features tendenziell schneller und effizienter konvergieren. Dies liegt daran, dass dadurch das Risiko einer schlechten Skalierung oder verschwindender Farbverläufe verringert wird.

Was sind die Normalisierungstechniken in Python?

Sie können die Normalisierung von NumPy- Arrays auf verschiedene Arten durchführen. Einige Methoden erfreuen sich aufgrund ihrer hohen Effizienz jedoch größerer Beliebtheit als andere.

In diesem Abschnitt betrachten wir die drei weit verbreiteten Normalisierungstechniken:

1. Min-Max-Skalierung

2. L1-Normalisierung

3. L2-Normalisierung

1. So führen Sie eine Min-Max-Skalierung durch

Die Min-Max-Skalierung wird auch als lineare Normalisierung oder Merkmalsskalierung bezeichnet. Bei der Min-Max-Skalierung skalieren wir die Werte eines NumPy-Arrays so, dass sie in einen bestimmten Bereich fallen, typischerweise zwischen 0 und 1.

Dazu subtrahieren Sie von jedem Element den Minimalwert und dividieren das Ergebnis durch die Differenz zwischen Maximal- und Minimalwert.

Sie können die Min-Max-Skalierung mathematisch wie folgt darstellen:

x' = (x - min(x)) / (max(x) - min(x))

Das folgende Beispiel zeigt, wie Sie mit der NumPy-Bibliothek eine Min-Max-Skalierung durchführen können:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)

scaled_matrix = (matrix - min_val) / (max_val - min_val)

print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)

Dieser Code importiert zunächst NumPy und berechnet dann die Mindest- und Höchstwerte in der Matrix, die er dann so skaliert, dass alle Werte zwischen 0 (entsprechend dem ursprünglichen Mindestwert) und 1 (entsprechend dem ursprünglichen Höchstwert) liegen.

Die Ausgabe dieses Codes ist unten angegeben:

Die Min-Max-Skalierung ist eine sehr verbreitete Form der Skalierung beim maschinellen Lernen und bei der Datenvorverarbeitung.

2. So führen Sie die L1-Normalisierung durch

Die L1-Normalisierung verwendet die L1-Norm, die die Summe der Absolutwerte der Array-Elemente ist. Dies ist besonders nützlich für dünn besetzte Matrizen. Es stellt sicher, dass die Summe der Absolutwerte der normalisierten Array-Elemente gleich 1 ist.

Die Formel für die L1-Normalisierung lautet:

x' = x / sum(|x|)

Das folgende Beispiel zeigt, wie Sie mit NumPy eine L1-Normalisierung durchführen können:

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm

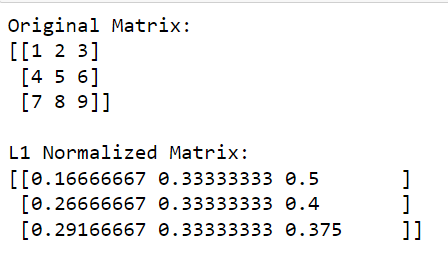
print('Original Matrix:')
print(matrix)
print('nL1 Normalized Matrix:')
print(l1_normalized_matrix)

In diesem Code berechnet np.linalg.norm (matrix, 1, axis=1, keepdims=True) die L1-Norm für jede Zeile (dies erfolgt durch Angabe von axis=1).

Diese Operation gibt einen Spaltenvektor zurück, in dem jedes Element die L1-Norm der entsprechenden Zeile ist. Indem wir die ursprüngliche Matrix durch diese Normen dividieren (wobei wir die Division elementweise durchführen), erhalten wir die L1-normalisierte Version der Matrix.

Die Ausgabe ist unten angegeben:

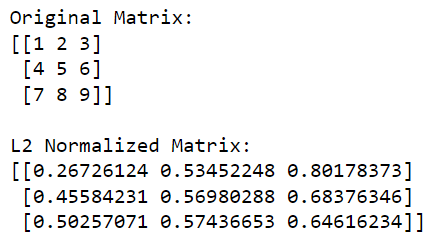
3. So führen Sie eine L2-Normalisierung durch

Die L2-Normalisierung verwendet die L2-Norm, die die Quadratwurzel der Summe der quadrierten Array-Elemente ist.

Diese Methode wandelt das normalisierte Array in einen Einheitsvektor mit einer 2-Norm von 1 um. Die L2-Normalisierung ist nützlich für die Dimensionsreduzierung und stellt die gleiche Wichtigkeit für alle Features sicher.

Die Formel für die L2-Normalisierung lautet:

x' = x / sqrt(sum(x^2))

So können Sie eine L2-Normalisierung mit NumPy durchführen :

import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm

print('Original Matrix:')
print(matrix)
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)

In diesem Code berechnet np.linalg.norm(matrix, 2, axis=1, keepdims=True) die L2-Norm (euklidische Norm) für jede Zeile (dies erfolgt durch Angabe von axis=1). Diese Operation gibt einen Spaltenvektor zurück, in dem jedes Element die L2-Norm der entsprechenden Zeile ist.

Indem wir die ursprüngliche Matrix durch diese Normen dividieren (wobei wir die Division elementweise durchführen), erhalten wir die L2-normalisierte Version der Matrix.

Die Ausgabe ist unten angegeben:

Okay, nachdem wir nun die gängigen Methoden zum Erstellen eines normalisierten Arrays mit NumPy besprochen haben, werfen wir im nächsten Abschnitt einen Blick darauf, wie Sie dasselbe mit anderen Python-Bibliotheken tun können.

So verwenden Sie Scikit-Learn zur Normalisierung in Python

Scikit-learn ist eine leistungsstarke Python-Bibliothek für maschinelles Lernen. Es stellt mehrere Tools zur Datenvorverarbeitung bereit.

Ein Tool, das Sie verwenden können, ist das Modul sklearn.preprocessing , das verschiedene Techniken zur Durchführung der Normalisierung bietet. Es stehen viele verschiedene Skalierungsfunktionen, Transformatoren und Normalisierer zur Verfügung. Wir konzentrieren uns jedoch auf MinMaxScaler und die Normalisierungsfunktion .

Um Daten mit scikit-learn vorzuverarbeiten, verwenden Sie hauptsächlich die Transformer-API. Dazu gehören die Methoden fit , transform und fit_transform .

1. So normalisieren Sie ein Array mit MinMaxScaler

Der MinMaxScaler ist ein Skalierer, der Daten auf einen angegebenen Bereich normalisiert, normalerweise [0, 1].

Die Formel für MinMaxScalar ist unten angegeben:

scaled_value = (value - min_value) / (max_value - min_value)

Um den MinMaxScaler zu implementieren , können Sie die folgenden Schritte ausführen:

1. Importieren Sie die erforderlichen Bibliotheken:

   import numpy as np
   from sklearn.preprocessing import MinMaxScaler

2. Erstellen Sie ein NumPy-Array:

   data = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])

3. Instanziieren Sie den MinMaxScaler und passen Sie ihn an die Daten an:

   scaler = MinMaxScaler()
   scaler.fit(data)

4. Transformieren Sie die Daten mit der Methode transform oder fit_transform :

   normalized_data = scaler.transform(data)

Die Ausgabe dieses Codes ist unten angegeben:

Wie Sie in der Ausgabe sehen können, hat die MinMaxScalarMatrix nur Werte im Bereich von 0 bis 1.

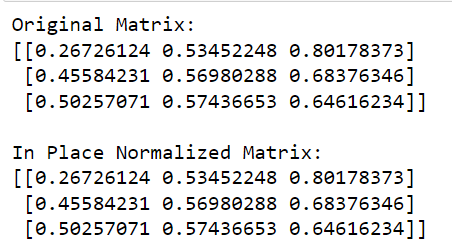
2. So führen Sie eine In-Place-Zeilennormalisierung durch

Alternativ können Sie auch die In-Place-Zeilennormalisierung verwenden, indem Sie die Normalisierungsfunktion verwenden .

Diese Methode normalisiert jedes Eingabearray oder jedes Eingabemerkmal unabhängig, indem der Vektor auf eine Einheitsnorm skaliert wird. Standardmäßig verwendet die Normalisierungsfunktion die L2-Norm, um eine einfache Normalisierung durchzuführen, Sie können jedoch auch andere Normoptionen auswählen.

Das folgende Beispiel veranschaulicht die direkte Zeilennormalisierung:

from sklearn.preprocessing import normalize
import numpy as np

# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)

# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)

print('L2 Normalized Matrix:')
print(matrix)

In diesem Code rufen wir die Normalisierungsfunktion von sklearn auf , definieren die zu verwendende Norm (in diesem Fall „l2“) und setzen copy=False, um eine direkte Normalisierung durchzuführen.

Die Ausgabe dieses Codes ist unten angegeben:

Um mehr über maschinelles Lernen in Python zu erfahren , schauen Sie sich das folgende Video an:

Abschließende Gedanken

Wenn Sie sich weiter mit Datenwissenschaft und maschinellem Lernen befassen, werden Sie feststellen, dass der Normalisierungsprozess ein wesentlicher Schritt in Ihrer Datenvorverarbeitungspipeline ist.

Erstens werden unterschiedliche Merkmale auf eine gemeinsame Skala gebracht. Dadurch reagieren Ihre Modelle weniger empfindlich auf den Maßstab der Eingaben. Es kann die Leistung vieler Algorithmen für maschinelles Lernen erheblich verbessern.

Zweitens hilft es Ihnen, den Trainingsprozess zu beschleunigen. Einige Algorithmen, insbesondere solche, die auf berechneten Entfernungsberechnungen basieren, konvergieren schneller, wenn Daten normalisiert werden.

Indem Sie lernen, Daten zu normalisieren, erwerben Sie eine entscheidende Fähigkeit. Die Normalisierung ist ein praktisches Werkzeug, das routinemäßig in realen Anwendungen eingesetzt wird. Dies hilft Ihnen dabei, die Wahrscheinlichkeit unerwarteter Ergebnisse aufgrund von Ausreißern oder Unterschieden in den Einheiten zu verringern.

Wie bei jedem Werkzeug liegt der Schlüssel zur Beherrschung der Normalisierung in der Praxis. Zögern Sie also nicht, sich die Hände schmutzig zu machen und mit verschiedenen Datensätzen und Zufallswerten zu experimentieren. Die Welt der Datenwissenschaft steht Ihnen offen. Viel Spaß beim Codieren!